 por Imscatman » Qui Mar 17, 2011 21:34
por Imscatman » Qui Mar 17, 2011 21:34
Prove que: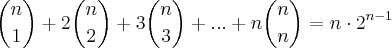
O livro até apresenta a solução, mas não compreendi:
Solução:Sabemos que:
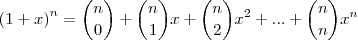
Derivando membro a membro em relação a

, temos:
[ñ entendi este passo]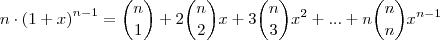
Fazendo

nesta igualdade resulta:
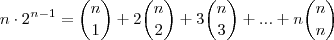
Até onde sei,
![n\cdot{(1+x)}^{n-1}=n\cdot\left[ {n-1 \choose 0} + {n-1 \choose 1}x + {n-1 \choose 2}{x}^{2} + ... + {n-1 \choose n-1}{x}^{n-1} \right] n\cdot{(1+x)}^{n-1}=n\cdot\left[ {n-1 \choose 0} + {n-1 \choose 1}x + {n-1 \choose 2}{x}^{2} + ... + {n-1 \choose n-1}{x}^{n-1} \right]](/latexrender/pictures/e91665a0de8efac5cff3c1672568ae15.png)
e não estou sabendo ver que isto seja o mesmo que
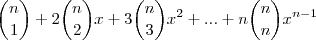
Se possível, gostaria de ver um passo-a-passo de como se chega da primeira coisa na segunda.
-

Imscatman
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mar 17, 2011 17:52
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Imscatman » Sáb Mar 19, 2011 12:45
por Imscatman » Sáb Mar 19, 2011 12:45
Nossa. Ou é muito difícil, ou muito fácil. Alguém poderia pelo menos me dizer qual é o caso? rsrs
-

Imscatman
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mar 17, 2011 17:52
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função]Não entendi
por Giudav » Sex Abr 13, 2012 00:30
- 1 Respostas
- 1435 Exibições
- Última mensagem por LuizAquino

Sáb Abr 14, 2012 12:20
Funções
-
- não entendi,ajudem-me?
por Amandatkm » Dom Mai 12, 2013 11:10
- 1 Respostas
- 2116 Exibições
- Última mensagem por Cleyson007

Dom Mai 12, 2013 14:26
Equações
-
- Prof nao entendi o q o sr escreveu
por gabimucedola » Seg Mar 29, 2010 14:25
- 3 Respostas
- 2036 Exibições
- Última mensagem por Elcioschin

Ter Mar 30, 2010 11:21
Álgebra Elementar
-
- [Simplificação Algébrica] Não entendi :(
por LucasMateusx » Qua Jan 04, 2017 12:19
- 2 Respostas
- 3432 Exibições
- Última mensagem por LucasMateusx

Qua Jan 04, 2017 14:40
Álgebra Elementar
-
- [Ajuda não entendi o enunciado] Limites
por elisafrombrazil » Sáb Jan 21, 2017 10:39
- 2 Respostas
- 5345 Exibições
- Última mensagem por e8group

Qua Fev 01, 2017 16:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
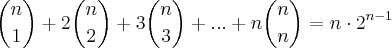
, temos:
nesta igualdade resulta:
![n\cdot{(1+x)}^{n-1}=n\cdot\left[ {n-1 \choose 0} + {n-1 \choose 1}x + {n-1 \choose 2}{x}^{2} + ... + {n-1 \choose n-1}{x}^{n-1} \right] n\cdot{(1+x)}^{n-1}=n\cdot\left[ {n-1 \choose 0} + {n-1 \choose 1}x + {n-1 \choose 2}{x}^{2} + ... + {n-1 \choose n-1}{x}^{n-1} \right]](/latexrender/pictures/e91665a0de8efac5cff3c1672568ae15.png)
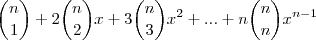

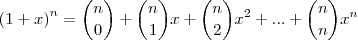
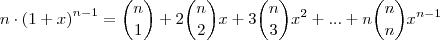
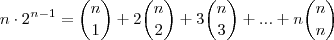

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.