 por natanskt » Ter Dez 07, 2010 13:36
por natanskt » Ter Dez 07, 2010 13:36
simpifique
(n-1)!+n!/(n+2)!
help
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por fttofolo » Ter Dez 07, 2010 21:02
por fttofolo » Ter Dez 07, 2010 21:02
(n-1)!+n!/(n+2)!
(n-1)!+n.(n-1)!/(n+2).(n+1).n.(n-1)!
(n-1)![1+n]/(n+2).(n+1).n.(n-1)! colocando (n-1)! em evidência
1+n/(n+2).(n+1).n
-
fttofolo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Sex Nov 19, 2010 10:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por luciana sanagioto » Ter Jun 28, 2011 15:40
por luciana sanagioto » Ter Jun 28, 2011 15:40
[Unparseable or potentially dangerous latex formula. Error 5 : 717x56]
natanskt escreveu:simpifique
(n-1)!+n!/(n+2)!
help
-
luciana sanagioto
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jun 28, 2011 11:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Ter Jun 28, 2011 20:27
por Molina » Ter Jun 28, 2011 20:27
Boa noite, Luciana.
luciana sanagioto escreveu:[Unparseable or potentially dangerous latex formula. Error 5 : 717x56]
natanskt escreveu:simpifique
(n-1)!+n!/(n+2)!
help
Vou escrever no LaTeX pois acho que assim o entendimento fica melhor:
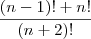
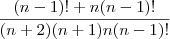 colocando no numerador o (n-1)! em evidência...
colocando no numerador o (n-1)! em evidência...![\frac{(n-1)![1+n]}{(n+2)(n+1)n(n-1)!} \frac{(n-1)![1+n]}{(n+2)(n+1)n(n-1)!}](/latexrender/pictures/0f8f8ee68f5ad2f9238ba7bc7fd2890e.png)
![\frac{[1+n]}{(n+2)(n+1)n} \frac{[1+n]}{(n+2)(n+1)n}](/latexrender/pictures/74b221dd5a9a2bb960bbbf960062e600.png) como 1 + n = n + 1...
como 1 + n = n + 1...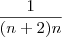
Qualquer dúvida informe!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplifique
por rodsales » Dom Ago 30, 2009 10:23
- 4 Respostas
- 12847 Exibições
- Última mensagem por Elcioschin

Dom Ago 30, 2009 14:32
Trigonometria
-
- Simplifique a expressão:
por andersontricordiano » Dom Jan 22, 2012 22:03
- 2 Respostas
- 7388 Exibições
- Última mensagem por laura1970

Ter Jun 11, 2013 10:50
Estatística
-
- Simplifique a Fração
por plugpc » Qui Mai 03, 2012 18:30
- 1 Respostas
- 1561 Exibições
- Última mensagem por DanielFerreira

Qui Mai 03, 2012 20:44
Sistemas de Equações
-
- [Potenciação] Simplifique
por SCHOOLGIRL+T » Qua Nov 07, 2012 21:29
- 2 Respostas
- 1383 Exibições
- Última mensagem por SCHOOLGIRL+T

Sex Nov 09, 2012 23:49
Álgebra Elementar
-
- simplifique as expressoes
por laura1970 » Seg Abr 22, 2013 16:03
- 3 Respostas
- 1767 Exibições
- Última mensagem por laura1970

Seg Abr 22, 2013 21:26
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





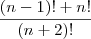
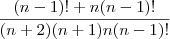
![\frac{(n-1)![1+n]}{(n+2)(n+1)n(n-1)!} \frac{(n-1)![1+n]}{(n+2)(n+1)n(n-1)!}](/latexrender/pictures/0f8f8ee68f5ad2f9238ba7bc7fd2890e.png)
![\frac{[1+n]}{(n+2)(n+1)n} \frac{[1+n]}{(n+2)(n+1)n}](/latexrender/pictures/74b221dd5a9a2bb960bbbf960062e600.png)
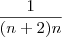

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.