 por GBT » Qui Mar 22, 2012 22:53
por GBT » Qui Mar 22, 2012 22:53
Olá, galera!
Tenho a seguinte amostra (representada em horas de trabalho):
325
254
256,5
122
178,5
212
25
Isso representa uma média de 196,14 e um desvio padrão de 91,76. Sei que é um desvio muito grande e que não posso afirmar nada com esses dados.
Um mês tem em média 160 horas úteis. Partindo disso, fiz uma regra de três simples:
160 -> 100%
91,76 -> x
Essa conta retorna 57,35%. Afinal, o que esse número representa? É correto afirmar que a dispersão estatística é de 57,35%?
-
GBT
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mar 22, 2012 22:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia
- Andamento: cursando
 por anabatista » Qua Abr 10, 2013 01:53
por anabatista » Qua Abr 10, 2013 01:53
Não!
o correto seria vc utilizar o coeficiente de variação de pearson
que diz o quanto a variação representa da média
e é dado pela forma simples de

o resultado é analisado da seguinte maneira, quanto menor mais homogeneos sao os dados, logo mais indicado.
No seu caso temos
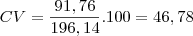
%
a partir dai vc pode dizer que a dispersao relativa é de aprox. 47% e isso é significativamente alto, ou seja, as horas de trabalho nao sao distribuidas de forma homogenea
-
anabatista
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Seg Abr 08, 2013 23:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por fernando7 » Dom Mai 13, 2018 21:55
por fernando7 » Dom Mai 13, 2018 21:55
46,7829101662 => 47%
-
fernando7
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Abr 11, 2018 20:31
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DESVIO PADRÃO E PORCENTAGEM] CÁLCULO
por scardao » Sáb Jun 14, 2014 16:07
- 0 Respostas
- 3540 Exibições
- Última mensagem por scardao

Sáb Jun 14, 2014 16:07
Estatística
-
- Desvio Padrão
 por Cleyson007 » Sáb Jun 13, 2009 11:18
por Cleyson007 » Sáb Jun 13, 2009 11:18
- 1 Respostas
- 4544 Exibições
- Última mensagem por Felipe Schucman

Qua Jul 29, 2009 02:22
Estatística
-
- Desvio padrão
por nina_0 » Dom Mai 08, 2011 19:04
- 1 Respostas
- 3203 Exibições
- Última mensagem por nina_0

Dom Mai 08, 2011 22:20
Estatística
-
- desvio padrao da media (SEM)
por lusasantos » Dom Mai 31, 2009 00:51
- 0 Respostas
- 2856 Exibições
- Última mensagem por lusasantos

Dom Mai 31, 2009 00:51
Estatística
-
- Probabilidade-Desvio Padrão
por veldri » Ter Abr 27, 2010 08:55
- 1 Respostas
- 5319 Exibições
- Última mensagem por Neperiano

Seg Jul 04, 2011 19:42
Dúvidas Pendentes (aguardando novos colaboradores)
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



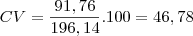 %
%