esse tipo de problema é classico... é como o problema duma sala com varias lampadas que podem ficar acesas ou apagadas... ou aquele das abelhas que podem ser macho ou femea, em fim... voce tem duas opçoes se intercalando... pode ser ou pto, ou traço... duas opções...
Se eu quero saber quantas opçoes eu tenho numa palavra de 3 letras, eu faço
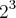
se eu quiser uma palavra de "n" letras
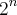
por que ?
no caso das 3 letras é por que na primeira casa eu tenho 2 opçoes... na segunda também duas, e na terceira duas tbm... dai
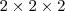
e no caso das "n" é análogo...
se eu preciso saber quantas palavras eu tenho com uma quantidade de letras que seja de uma até 3 eu tenho que somar a quantidade de palavras com uma, à quantidade de palavras com duas, à quantidade de palavras com 3...
se eu preciso da quantidade de palavras possiveis com um numero de 1 até "n" letras eu tenho que somar todas as possbilidades de palavras de 1 letra, depois de 2, depois de 3 depois 4 ... até chegar em n
Baseado nisso, tente fazer o exercicio.


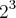
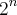
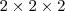
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
