-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478492 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 533198 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 496708 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 709741 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2128553 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Flavia R » Qua Set 28, 2011 17:49
por Flavia R » Qua Set 28, 2011 17:49
Ana dispunha de papéis com cores diferentes. Para enfeitar sua loja cortou fitas desses papéis e embalou 30 caixinhas de modo a não usar a mesma cor no papel e na fita, em nenhuma das 30 embalagens. A menor quantidade de cores diferentes que ela necessitou utilizar para a confecção de todas as embalagens foi igual a :
resposta= 6
não entendo o motivo, por mim 3 papéis diferentes já dava para fazer todas as caixinhas.
-
Flavia R
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Ago 24, 2011 17:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso técnico em agrimensura
- Andamento: formado
 por Neperiano » Qui Set 29, 2011 16:24
por Neperiano » Qui Set 29, 2011 16:24
Ola
Quantos lados uma caixa têm? 6
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por jose henrique » Qua Out 26, 2011 21:32
por jose henrique » Qua Out 26, 2011 21:32
olá boa noite!!
percebemos que o papel e a fita para essas 30 caixas deverão ser distintos, ou seja a cor que eu usar para um eu não posso usar para o outro. essa combinação n cores dará um grupo de 30 caixas.então podemos formar pelo principio multiplicativo que:
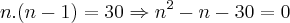
desenvolvendo a equação, podemos que a solução da mesma é :
S={-5, 6}
podemos perceber que o valor que nos interessa é apenas o 6.
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão de Análise Combinatória
por Felipe55 » Qua Jul 06, 2011 05:13
- 1 Respostas
- 2400 Exibições
- Última mensagem por MarceloFantini

Qua Jul 06, 2011 20:27
Estatística
-
- Análise combinatoria questão
por kariarita » Qui Ago 11, 2011 12:55
- 1 Respostas
- 1980 Exibições
- Última mensagem por Caradoc

Sáb Ago 13, 2011 16:56
Estatística
-
- QUESTÃO DE ANÁLISE COMBINATÓRIA
por Matpas » Ter Ago 25, 2015 16:00
- 2 Respostas
- 6727 Exibições
- Última mensagem por Matpas

Ter Ago 25, 2015 21:06
Análise Combinatória
-
- QUESTÃO DE ANÁLISE COMBINATÓRIA
por mgomury » Sex Jun 17, 2016 14:16
- 1 Respostas
- 7054 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 18, 2016 18:12
Análise Combinatória
-
- [Dúvida] Questão ITA análise combinatória
por birondon » Sex Mar 23, 2012 01:13
- 1 Respostas
- 2232 Exibições
- Última mensagem por fraol

Seg Mar 26, 2012 23:01
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 18 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 , avisa que eu resolvo.
, avisa que eu resolvo.

