 por Brainwreck » Qua Ago 31, 2011 19:45
por Brainwreck » Qua Ago 31, 2011 19:45
Boas pessoal,
Tenho uma duvida em um problema que é o seguinte:
(copiado na integra)
"A Maria gravou nove CD, sete com música rock e dois com música popular, mas esqueceu-se de identificar cada um deles.
Qual é a probabilidade de, ao escolher dois CD ao acaso, um ser música rock e o outro ser de música popular?
-- A questão dá a solução que é "7/18" mas não sei como chegar a essa conclusão.
Obrigado pela ajuda.
-
Brainwreck
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Ago 31, 2011 19:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Caradoc » Qua Ago 31, 2011 22:47
por Caradoc » Qua Ago 31, 2011 22:47
Pensei desta forma:
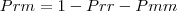
Ou seja, o total (100%) - a probalidade de pegar só rock ou só música popular.
A probabilidade de pegar só rock é:
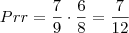
e a probabilidade de pegar só música popular é:
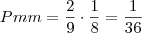
Logo a probabilidade de pegar um de cada é:
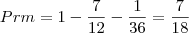
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Probabilidades - problema
por emsbp » Qui Jun 07, 2012 17:57
- 5 Respostas
- 13833 Exibições
- Última mensagem por SARAABRANCO

Qua Jun 13, 2012 17:57
Probabilidade
-
- [Probabilidades e análise combinatória] Problema
por fff » Qua Mar 05, 2014 16:59
- 0 Respostas
- 1312 Exibições
- Última mensagem por fff

Qua Mar 05, 2014 16:59
Análise Combinatória
-
- Probabilidades - cálculo probabilidades e condicionada
por carlosmartins » Dom Set 21, 2014 18:58
- 0 Respostas
- 2957 Exibições
- Última mensagem por carlosmartins

Dom Set 21, 2014 18:58
Probabilidade
-
- probabilidades
 por edwilsoncrep » Qui Mar 04, 2010 19:28
por edwilsoncrep » Qui Mar 04, 2010 19:28
- 3 Respostas
- 3292 Exibições
- Última mensagem por edwilsoncrep

Qui Mar 04, 2010 19:49
Estatística
-
- Probabilidades!
por pferraz » Qui Out 27, 2011 22:53
- 3 Respostas
- 7076 Exibições
- Última mensagem por Russman

Qua Dez 23, 2015 22:04
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


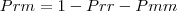
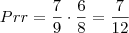
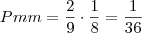
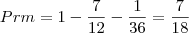


 .
.



