Numa cidade,os números de telefone são formados de um prefixo de 3 algarismos,seguidos de outros 4 algarismos.O primeiro algarismo do prefixo é sempre um elemento do conjunto {2,3,5,6,7,8,9} os demais algarismos são quaisquer.Nessas condições quer- se saber
a)Quantos telefones podem ser instalados nessa cidade?
b) quantos números de telefone tem os 4 algarismos finais distintos?
c) quantos números de telefone tem o primeiro dos 4 algarismos diferente de zero ?
d) Quantos números de telefone tem os 4 algarismos finais distintos e o primeiro desses 4 diferente de zero?
Bem.. eu fiz o seguinte :
a) como o primeiro algarismo deve ser um elemento do conjunto temos 7 possibilidades Então 7.10^6 = 7.000.000
b) eu tinha feito assim : 7. 10.9.8.7 mas no gabarito está 7.10^3.9.8.7 = 3.528.000 alguém pode me explicar?
c) a letra " c e d" eu não entendi nada...


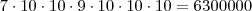
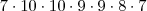


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)