O número de anagramas da palavra concurso que começam com a letra R? Resp- 1260
Qdo a palavra não tem letras repitidas eu faço por permutação simples e qdo tem letras repetidas como faço para encontrar o número de anagramas?



Rejane Sampaio escreveu:O número de anagramas da palavra concurso que começam com a letra R? Resp- 1260
Qdo a palavra não tem letras repitidas eu faço por permutação simples e qdo tem letras repetidas como faço para encontrar o número de anagramas?
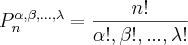
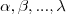 são as repetições e
são as repetições e 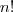 é o número total de letras da palavra.
é o número total de letras da palavra.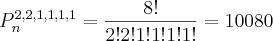
 Obs.: as letras que não se repetem normalmente nao colocadas. Já que 1! = 1, e como estamos multiplicando nao faz diferença. Sendo assim a formula da questão poderia ser escrita assim:
Obs.: as letras que não se repetem normalmente nao colocadas. Já que 1! = 1, e como estamos multiplicando nao faz diferença. Sendo assim a formula da questão poderia ser escrita assim: 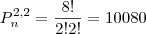



Usuários navegando neste fórum: Nenhum usuário registrado e 21 visitantes
