Olá Rejane!
Molina, sobre o fatorial, parece que a Rejane quis escrever assim:
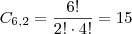
Pensei no problema e comento o seguinte:
Como pede-se o "número de possibilidades que
você tem de ser premiado", dentre as 7 pessoas, de início já consideramos uma pessoa com prêmio,
você.
Então, os 2 prêmios restantes ficarão entre as 6 pessoas restantes.
Refazendo a pergunta, temos: de quantas maneiras os 2 prêmios podem ser sorteados entre as 6 pessoas?
Daí a combinação
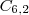
.
Note que aqui pode haver outra dúvida que é a seguinte:
Por que não arranjos

, já que os prêmios são
diferentes, e a ordem fará diferença para os premiados?

Pois é, a ordem dos 2 outros prêmios fará diferença para os 6 outros premiados, mas não para
você.
Mas agora,
eu deixo outra dúvida pendente: o número de possibilidades ainda não teria que ser multiplicado por 3 (ou somado 3 vezes)?
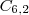
são as possibilidades de premiação caso
você receba um
prêmio do tipo 1 (sendo distribuídos os prêmios 2 e 3).
ou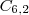
são as possibilidades de premiação caso
você receba um
prêmio do tipo 2 (sendo distribuídos os prêmios 1 e 3).
ou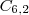
são as possibilidades de premiação caso
você receba um
prêmio do tipo 3 (sendo distribuídos os prêmios 1 e 2).
Até mais!




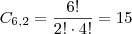
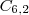 .
. , já que os prêmios são
, já que os prêmios são 

 através dessas possibilidades já posso fazer uma outra análise da questão.
através dessas possibilidades já posso fazer uma outra análise da questão.
 .
.



