-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480283 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 540133 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 503999 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 729193 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2166437 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Roberta » Qui Jun 26, 2008 21:53
por Roberta » Qui Jun 26, 2008 21:53
ola!

Gostaria de pedir a ajuda do *pessoal* para a resolução (de forma bem simples) do seguinte problema:
Temos quatro urnas, cada uma contendo dez bolas numeradas de 0 a 9. Sorteando ao acaso uma bola de cada uma, formamos um número entre 0 e 9999. Lembrando que zero é multiplo de qualquer número inteiro, determine a probabilidade de o número sorteado ser múltiplo de 8.
a) 7,8%
b) 8.5%
c) 13%
d) 12,5%
e) 15,5%
O gabarito eu tenho... levei horas pra fazer ... e tentar estabelecer uma sequência lógica para os múltiplos de 8. Mas gostaria de saber qual a forma simples e rápida que vcs usariam para resolver, caso fosse uma questão de prova?
Obrigada!!
Roberta.gmail

-
Roberta
- Usuário Parceiro

-
- Mensagens: 56
- Registrado em: Qui Jun 19, 2008 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: estudante de direito
- Andamento: cursando
 por Molina » Sex Jun 27, 2008 00:29
por Molina » Sex Jun 27, 2008 00:29
Boa noite, Roberta.
Tudo bem?
Eu faria da segunte maneira:
A quantidade de urnas nao nos importa, o importante mesmo sao os números que elas podem formas. Temos as possibilidades de 0 à 9999, ou seja, dez mil possibilidades.
Segundo passo é ver quanto múltiplos de 8 existem entre 0 e 9999. Basta dividir 9999 por 8 e pegar o número inteiro (1249). Só que o problema relembra que o 0 é múltiplo de todos os números, ou seja, 1249 + 1 = 1250.
Em probabilidade temos que quocientar o número de evento que desejamos pelo número de eventos possíveis. Nessas condições teríamo:
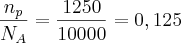
Ou seja, 12,5%
(não consegui fazer o símbolo do % no LaTeX)
Bom estudo!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Roberta » Sex Jun 27, 2008 01:21
por Roberta » Sex Jun 27, 2008 01:21
Nosssssssssssssssssssssss... molina!

Valeu mesmo! vc precisa ver qtos cálculos inúteis eu fiz!! kkkkkkkkkkk

E obtive numero de multiplos diferente deste... deu 2.750


mas estes cálculos fazem mais sentido!
VlW!!
Roberta.gmail

-
Roberta
- Usuário Parceiro

-
- Mensagens: 56
- Registrado em: Qui Jun 19, 2008 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: estudante de direito
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade] Exercício Desafio de Probabilidade
por werwer » Qua Mar 21, 2012 18:57
- 0 Respostas
- 9785 Exibições
- Última mensagem por werwer

Qua Mar 21, 2012 18:57
Estatística
-
- Probabilidade - Função Densidade de Probabilidade
por pimgui » Qua Dez 16, 2020 10:53
- 0 Respostas
- 14626 Exibições
- Última mensagem por pimgui

Qua Dez 16, 2020 10:53
Probabilidade
-
- Probabilidade - função probabilidade
por tarlix » Ter Mai 24, 2011 12:41
- 1 Respostas
- 4710 Exibições
- Última mensagem por Neperiano

Dom Out 16, 2011 17:00
Estatística
-
- [Probabilidade] probabilidade de obj com estudantes
por fenixxx » Seg Ago 13, 2012 14:06
- 1 Respostas
- 4005 Exibições
- Última mensagem por Neperiano

Ter Out 09, 2012 10:10
Probabilidade
-
- [probabilidade condicional] probabilidade de gol.
 por Mr_ MasterMind » Sáb Set 19, 2015 17:35
por Mr_ MasterMind » Sáb Set 19, 2015 17:35
- 0 Respostas
- 4108 Exibições
- Última mensagem por Mr_ MasterMind

Sáb Set 19, 2015 17:35
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 17 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


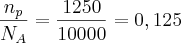

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.