por Mariela_Brito » Qui Mai 07, 2020 17:33
Olá pessoal,
Estou com uma grande dúvida relacionada ao cálculo de variação percentual.
Eu trabalho com dados agricolas para a produção de grãos, dados estes advindos do IBGE. Assim, gostaria de mostrar como a produção de grãos está variando de um ano para outro. Fazendo então uma pesquisa encontrei a fórmula da variação percentual, [(valor final/ valor inicial) - 1] * 100, que poderia me servir como resposta. Porém todos os exempls que vejo são desta fórmula para a área financeira, ou seja referente a calculos monetarios.
calculo a variação acumulada entre os anos?
Se não posso fazer esta aplicação, poderiam me informar alguma outra forma e bibliografia que poderia utilizar?
Abaixo deixo um exemplo caso possam me ajudar.
PRODUÇÃO (Tonelada)
ANO MILHO SOJA
2009 210000 99000
2010 250000 120500
2011 71000 20000
2012 298800 140050
2013 172000 189600
-
Mariela_Brito
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Qua Mai 06, 2020 17:37
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: GEOGRAFIA
- Andamento: cursando
por Baltuilhe » Seg Mai 11, 2020 20:22
Boa noite!
Pode montar da seguinte forma:
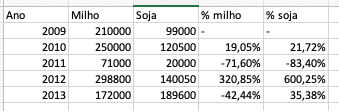
- Tabela
- Captura de Tela 2020-05-11 a?s 18.18.05.png (12.73 KiB) Exibido 5188 vezes
O cálculo começa em '-' pois 2009 foi tomado como ano inicial, não tem referência.
Para 2010 toma-se o valor de 2010 e divide-se pelo valor de 2009, subtraindo-se 1:
250000/210000-1=1,1905-1=0,1905=19,05%
O mesmo para os outros!
-
Baltuilhe
- Usuário Parceiro
-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Variação Percentual]
por Wilson Rogerio Braun » Sex Ago 26, 2011 21:29
- 4 Respostas
- 3976 Exibições
- Última mensagem por Wilson Rogerio Braun
Seg Ago 29, 2011 13:59
Álgebra Elementar
-
- Taxa de variação percentual
por marilia07 » Seg Out 15, 2012 20:46
- 2 Respostas
- 4852 Exibições
- Última mensagem por marilia07
Seg Out 15, 2012 21:56
Cálculo: Limites, Derivadas e Integrais
-
- Inflação acumulada
por Catriane Moreira » Dom Nov 07, 2010 17:24
- 1 Respostas
- 1954 Exibições
- Última mensagem por Elcioschin
Dom Nov 07, 2010 22:33
Matemática Financeira
-
- Distribuição Acumulada de probabilidade
por LeoLemos123 » Qui Mai 11, 2017 20:50
- 0 Respostas
- 2640 Exibições
- Última mensagem por LeoLemos123
Qui Mai 11, 2017 20:50
Estatística
-
- Produção;
por pedro_s_n » Sex Jun 24, 2011 15:44
- 1 Respostas
- 2035 Exibições
- Última mensagem por MarceloFantini
Sex Jun 24, 2011 17:35
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
