 por elisafrombrazil » Ter Jan 24, 2017 11:42
por elisafrombrazil » Ter Jan 24, 2017 11:42
Dada a distribuição abaxio, mostre que a soma dos desvios = 0.
82 89 94 110 74 122 112 95 100 78 65 60
90 83 87 75 114 85 69 94 124 115 197 88
97 74 72 68 83 91 90 102 77 125 108 65
-
elisafrombrazil
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sáb Dez 31, 2016 10:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Docente » Seg Out 16, 2017 16:25
por Docente » Seg Out 16, 2017 16:25
Primeiro você faz a média dos dados

Depois faz o desvio da media que é Xi-

(Xi São os valores 82,89, 94... todos os valores)
logo apos faz o somatório de todos os desvios dos valores
pois o
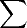
dos desvios dos valores é =0;
-
Docente
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 16, 2017 16:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Estatistica descritiva escores e desvios
por Docente » Seg Out 16, 2017 16:15
- 0 Respostas
- 5305 Exibições
- Última mensagem por Docente

Seg Out 16, 2017 16:15
Estatística
-
- Mostre que:
por Cleyson007 » Seg Jul 11, 2011 22:09
- 1 Respostas
- 1737 Exibições
- Última mensagem por LuizAquino

Ter Jul 12, 2011 09:43
Cálculo: Limites, Derivadas e Integrais
-
- Mostre que:
por Cleyson007 » Sex Abr 27, 2012 12:23
- 1 Respostas
- 1695 Exibições
- Última mensagem por Guill

Sex Abr 27, 2012 21:39
Cálculo: Limites, Derivadas e Integrais
-
- [Mostre] que
por NicoleNicolela » Qua Abr 10, 2013 20:15
- 2 Respostas
- 2487 Exibições
- Última mensagem por e8group

Qua Abr 10, 2013 23:49
Funções
-
- [MDC] Mostre que, ?n ? Z, o mdc( 2n+1 , n(n+1)/2) = 1
por ferfer » Dom Mai 26, 2013 13:38
- 5 Respostas
- 4020 Exibições
- Última mensagem por ferfer

Qui Mai 30, 2013 13:22
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





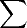 dos desvios dos valores é =0;
dos desvios dos valores é =0;
