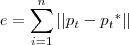por brunozi » Ter Set 29, 2009 10:54
por brunozi » Ter Set 29, 2009 10:54
Olá, pessoal,
Estou com um problema que envolve a estimação de posição e orientação de um objeto no espaço 3D, a partir de sua projeção 2D, no caso, um frame de vídeo, supondo conhecida a posição e orientação no frame anterior.
O problema é o seguinte:
Tenho alguns pontos 3D do objeto no instante (t-1):
![{P}_{i, t - 1} = {[ {X}_{i, t - 1} {Y}_{i, t - 1} {Z}_{i, t - 1} 1 ]}^{T} {P}_{i, t - 1} = {[ {X}_{i, t - 1} {Y}_{i, t - 1} {Z}_{i, t - 1} 1 ]}^{T}](/latexrender/pictures/81923f1d4825ecc50bda0a3e27463078.png)
Tenho os correspondentes pontos 2D no instante t:
![{p}_{i, t} = {[ {x}_{i, t } {y}_{i, t} ]}^{T} {p}_{i, t} = {[ {x}_{i, t } {y}_{i, t} ]}^{T}](/latexrender/pictures/dc3024dabc601f58927465b3c336cc39.png)
A transformação dos pontos do instante (t - 1) para o instante t é calculada por:

E a projecão 2D desses pontos é calculada por:
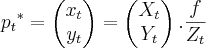
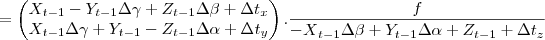
O objetivo é encontrar o valor de
![\Delta\mu = {[\Delta\alpha \Delta\beta \Delta\gamma \Delta{t}_{x} \Delta{t}_{y} \Delta{t}_{z} ]}^{T} \Delta\mu = {[\Delta\alpha \Delta\beta \Delta\gamma \Delta{t}_{x} \Delta{t}_{y} \Delta{t}_{z} ]}^{T}](/latexrender/pictures/65518e4b5873dddb0e41eb01e3f973e1.png)
que minimize o erro:
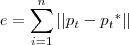
O problema é que ainda não consegui ver como aplicar mínimos quadrados a esse problema, que tem parâmetros tanto no numerados como no denominador.
É possível aplicar mínimos quadrados a um problema desse tipo? Como posso fazer isso? Ou, onde posso encontrar informações sobre como fazer isso?
Obrigado.
-
brunozi
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Set 29, 2009 09:26
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: M.Sc. Eng. de Computação
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Mínimos quadrados e Projeção Ortogonal
por Jhonata » Sex Jul 19, 2013 19:44
- 7 Respostas
- 5213 Exibições
- Última mensagem por Jhonata

Dom Jul 21, 2013 10:49
Álgebra Linear
-
- Método dos Mínimos Quadrados - Dúvida no desenvolvimento
por cafdesouza » Dom Dez 11, 2011 11:36
- 0 Respostas
- 1271 Exibições
- Última mensagem por cafdesouza

Dom Dez 11, 2011 11:36
Estatística
-
- Minimos Quadrados e Curva S , descobrir coef a e b
por Joao Petrocelle » Qui Jan 17, 2013 10:00
- 0 Respostas
- 1078 Exibições
- Última mensagem por Joao Petrocelle

Qui Jan 17, 2013 10:00
Funções
-
- Problema, mínimos e máximos
por Bruhh » Sex Jun 11, 2010 16:45
- 3 Respostas
- 2692 Exibições
- Última mensagem por Bruhh

Sex Jun 11, 2010 16:53
Cálculo: Limites, Derivadas e Integrais
-
- área de quadrados
por Nane » Dom Out 31, 2010 09:38
- 0 Respostas
- 2548 Exibições
- Última mensagem por Nane

Dom Out 31, 2010 09:38
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{P}_{i, t - 1} = {[ {X}_{i, t - 1} {Y}_{i, t - 1} {Z}_{i, t - 1} 1 ]}^{T} {P}_{i, t - 1} = {[ {X}_{i, t - 1} {Y}_{i, t - 1} {Z}_{i, t - 1} 1 ]}^{T}](/latexrender/pictures/81923f1d4825ecc50bda0a3e27463078.png)
![{p}_{i, t} = {[ {x}_{i, t } {y}_{i, t} ]}^{T} {p}_{i, t} = {[ {x}_{i, t } {y}_{i, t} ]}^{T}](/latexrender/pictures/dc3024dabc601f58927465b3c336cc39.png)

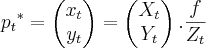
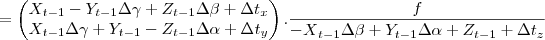
![\Delta\mu = {[\Delta\alpha \Delta\beta \Delta\gamma \Delta{t}_{x} \Delta{t}_{y} \Delta{t}_{z} ]}^{T} \Delta\mu = {[\Delta\alpha \Delta\beta \Delta\gamma \Delta{t}_{x} \Delta{t}_{y} \Delta{t}_{z} ]}^{T}](/latexrender/pictures/65518e4b5873dddb0e41eb01e3f973e1.png) que minimize o erro:
que minimize o erro: