Olá. Olha, eu resolvi a sua questão apesar de já fazer mais de um mês que você enviou. Não sei se o que eu fiz está correto, mas vou mostrar o meu raciocínio.
Se o hospital teve um gasto trimestral constante de 10.000€ naquele ano, então podemos dividir este por 4, já que temos 4 trimestres num ano. Daí, resulta em 2500 o gasto em cada trimestre. Há também a informação de que as seringas foram vendidas pelos seguintes valores, em cêntimos de unidade (ou seja, um centésimo da moeda usada):
1º trimestre:55
2º trimestre:60
3º trimestre:65
4º trimestre:90
De onde podemos concluir que no 1º trimestre, cada seringa foi cobrada num valor de 0,55; no 2º, de 0,60; no 3º, de 0,65; no 4º, de 0,90.
Isto significa que:
x = quantidade de seringas adquiridas no 1º trimestre;
y = quantidade de seringas adquiridas no 2º trimestre;
k = quantidade de seringas adquiridas no 3º trimestre;
p = quantidade de seringas adquiridas no 4º trimestre;
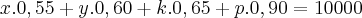
Então, podemos fazer o seguinte:
x.0,55 = 2500

x

454
y.0,60 = 2500

x

416
k.0,65 = 2500

x

384
p.0,90 = 2500

x

277
Daí,
454 + 416 + 384 + 277 = 1531
E,
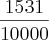

0,15
Espero que o gabarito seja: um preço médio de 0,15 por seringa.
Desculpe se estiver errado!


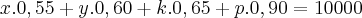
 x
x  454
454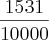


 .
.
 :
: