 por caducustodio » Qua Ago 15, 2012 19:03
por caducustodio » Qua Ago 15, 2012 19:03
DE ACORDO COM ESTUDOS ESTATÍSTICOS REALIZADOS, A QUANTIDADE DE HABITANTES DE UMA DETERMINADA REGIÃO DEVE AUMENTAR, NOS PRÓXIMOS ANOS, DE ACORDO COM A FUNÇÃO P(t) = 83.000 . 1,03t, ONDE P(t) É A QUANTIDADE (APROXIMADA DE HABITANTES DAQUI A t ANOS.
a-) QUAL DEVE SER A QUANTIDADE PROVÁVEL (E APROXIMADA) DE HABITANTES DESSA REGIÃO DAQUI A 7 ANOS?
b-) QUANTOS ANOS (APROXIMADAMENTE) SERÃO NECESSÁRIOS PARA QUE A POPULAÇÃO DESSA REGIÃO DOBRE DE TAMANHO?
OBS.: UTILIZE 5 CASAS DECIMAIS NOS CÁLCULOS.
-
caducustodio
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Ago 15, 2012 18:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por MarceloFantini » Qua Ago 15, 2012 20:05
por MarceloFantini » Qua Ago 15, 2012 20:05
Para a letra (a) basta substituir

.
Para a letra (b) faça
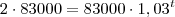
e resolva para

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Graficos estatisticos e Funcoes
por j_cruz » Qui Fev 11, 2010 18:16
- 1 Respostas
- 2905 Exibições
- Última mensagem por Molina

Qui Fev 11, 2010 21:36
Estatística
-
- Grupo de Estudos
por Thiago Silveira » Ter Set 21, 2010 18:12
- 3 Respostas
- 3382 Exibições
- Última mensagem por nietzsche

Qui Set 01, 2011 23:55
Pedidos
-
- Qual o plano de estudos?
por joaofonseca » Qui Dez 29, 2011 09:43
- 2 Respostas
- 3902 Exibições
- Última mensagem por joaofonseca

Qua Fev 08, 2012 21:45
Educação Matemática
-
- Grupo para estudos
por edsongsrj » Qua Fev 13, 2013 21:52
- 0 Respostas
- 2056 Exibições
- Última mensagem por edsongsrj

Qua Fev 13, 2013 21:52
Pedidos de Materiais
-
- Dicas de livros e material de estudos
por wmax » Sex Ago 02, 2013 00:00
- 1 Respostas
- 2097 Exibições
- Última mensagem por temujin

Sex Ago 02, 2013 12:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
.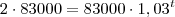 e resolva para
e resolva para  .
.
