 por tigerwong » Dom Jun 24, 2012 21:07
por tigerwong » Dom Jun 24, 2012 21:07
Estou precisando dessa questão, pois os dias para entrar com recursos começa amanhã. Apenas sei resolver combinção simples e não com repetição desse tipo:
1) (Prefeitura de Bayeux - 2012) A fachada de um edifício é formada por 7 listras que vão ser coloridas usando-se as cores: lilás, rosa e vermelha. Se cada listra deve ter apenas uma cor e não podem ser usadas cores iguais em listras adjacentes, de quantos modos é possível colorir esta fachada?
a)192
b)108
c)22187
d)648
e)128
-
tigerwong
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Jun 24, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por danyeleal » Ter Jun 26, 2012 04:06
por danyeleal » Ter Jun 26, 2012 04:06
TIGERWONG, EU TAMBÉM FIZ ESSA PROVA E PELOS MEUS CÁLCULOS DARIA 2187, MAS NA ALTERNATIVA C) ESTAVA 22187. QUERIA SABER SE ALGUÉM CONSEGUIU ACERTAR ESSA QUESTÃO, POIS FIQUEI COM VONTADE DE RECORRER.
-
danyeleal
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jun 26, 2012 03:48
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por EMCM » Ter Jun 26, 2012 06:58
por EMCM » Ter Jun 26, 2012 06:58
Vamos tratar cada lista por (-----):
Aqui podem ser utilizadas todas as 3 cores, portanto
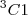
1ª --------
Nestes restantes, como não se pode repetir a cor anterior, escolhe-se apenas de 2 cores, fica
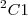
2ª --------
3ª --------
4ª --------
5ª --------
6ª --------
7ª --------
Então é possivel colorir a fachada de
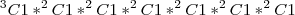
=
192
-
EMCM
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Jun 24, 2012 14:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por tigerwong » Ter Jun 26, 2012 10:29
por tigerwong » Ter Jun 26, 2012 10:29
A resposta correta, conforme o gabarito, é a letra "e"
-
tigerwong
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Jun 24, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
 por danyeleal » Ter Jun 26, 2012 13:10
por danyeleal » Ter Jun 26, 2012 13:10
Obrigada, pela explicação! A resposta confirma o gabarito preliminar do concurso: Letra a).
-
danyeleal
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Jun 26, 2012 03:48
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por tigerwong » Ter Jun 26, 2012 14:18
por tigerwong » Ter Jun 26, 2012 14:18
danyeleal escreveu:Obrigada, pela explicação! A resposta confirma o gabarito preliminar do concurso: Letra a).
Tem razão, foi mal
-
tigerwong
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Jun 24, 2012 20:49
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Analise Combinatoria - Questao de Combinacao
por casmota » Sex Mar 23, 2018 10:31
- 2 Respostas
- 5604 Exibições
- Última mensagem por casmota

Sáb Mar 24, 2018 12:18
Análise Combinatória
-
- Análise combinatória (combinação) - questão desafiadora....
por d7carvalho » Dom Ago 29, 2010 00:41
- 1 Respostas
- 2052 Exibições
- Última mensagem por Douglasm

Dom Ago 29, 2010 15:37
Estatística
-
- Repetição lotérica
por andre Luiz » Qua Fev 16, 2011 11:07
- 2 Respostas
- 1944 Exibições
- Última mensagem por EMCM

Ter Jun 26, 2012 06:43
Probabilidade
-
- [Combinação de Numeros]Combinação até chegar em outro
por moacirrf » Dom Set 30, 2012 15:51
- 0 Respostas
- 1790 Exibições
- Última mensagem por moacirrf

Dom Set 30, 2012 15:51
Análise Combinatória
-
- Sucessão e quantidade de vezes de repetição de algarismo
por remoreiraaa » Qua Jan 06, 2010 20:26
- 1 Respostas
- 3602 Exibições
- Última mensagem por Molina

Sex Jan 08, 2010 13:53
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



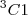
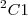
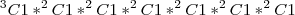 =
=  em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.