Na caixa A existem 12 bombons, dos quais 5 sem recheio.Na caixa B existem 6 bombons dos quais 2 sem recheio.Retirando 1 bombon de cada caixa, qual é a probabilidade de um ter recheio e o outro não?
A partir do enunciado deduzi logo que a ordem pela qual os bombons são retirados das caixas não é relevante.
Primeiro defeni alguns acontecimentos:
A-"Retirar um bombon da caixa A".
Deduz-se que
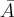será retirar um bombom da caixa B.R-"Retirar um bobom com recheio".
Depois escrevi:
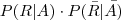
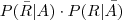
Estas probabilidades refletem as duas situações:
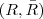e 
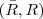.O resultado foi
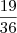.Mas não coincide com o gabarito que é de 
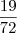.Depois ainda desenhei uma tabela de dupla entrada.Procedendo depois ao produto/soma:
Os casos favoráveis serão:
Estou a partir do principio que os casos possiveis são 72.
Onde estou a errar?
, 
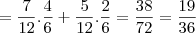por alexandre32100 » Qui Set 09, 2010 21:10
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.