Andreza escreveu:Quantos são os números pares entre 1000 e 9999 que consistem de 4 algarismos distintos?
Neste exercício eu estou em dúvida sobre o q usar: Arranjo, combinação ou apenas permutação.
Desde já agradeço.
Olá Andreza.
Como a ordem importa, ou é arranjo ou permutação. Como não se utiliza todos os algarismos (1 a 9) de uma vez, pois serão formados números de 4 algarismos, é um
arranjo.
Você pode resolver este exercício, encontrando os números que terminam em 0, 2, 4, 6 ou 8.
Seria também interessante encontrar os números que terminam em 0 primeiro, pois o número formado não poderá começar com 0.
1º caso (terminando em 0):_ _ _ 1

9_ _ 1
 2º caso (terminando em 2, 4, 6 ou 8):
2º caso (terminando em 2, 4, 6 ou 8):_ _ _ 4

8 _ _ 4 (a primeira casa deve conter um número diferente do da última e diferente de 0. 10 - 2 = 8)

8 8 _ 4 (a segunda casa deve ser diferente dos algarismos da última casa e da primeira casa, mas pode conter o zero. 8 - 1 + 1 = 8)
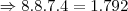
Somando
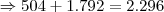
Qualquer dúvida...



 9_ _ 1
9_ _ 1 
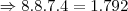
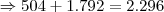

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)