Olha, vê se compreende meu raciocínio, pois essa deu um pouco de trabalho. Não sei se é o método correto mas funcionou (eu acho)...
Vamos lá então.
Primeiro, chamaremos de
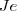
a calça jeans,
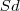
o sapato direito,

o sapato esquerdo,
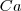
a camisa e
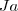
a jaqueta.
Assim podemos perceber, levando em consideração as condições do problema, o seguinte:
devemos fixar as peças de roupa que são condicionantes, ou seja,
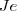
e
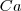
, logo teremos as seguintes configurações de ordem na sequência de peças
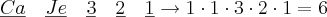
modos diferentes
ou seja, veste-se primeiro com a camisa, depois com a calça jeans, em seguida poderá ser escolhida qualquer peça, entre

,
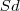
e
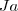
, uma de cada vez.

modos diferentes
ou seja, veste-se primeiro com a camisa, depois com a
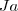
, daí a calça jeans, em seguida poderá ser escolhida qualquer peça, entre

,
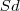
.

modos diferentes
ou seja, veste-se primeiro com a calça jeans, depois com a camisa, em seguida poderá ser escolhida qualquer peça, entre

,
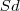
e
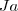
, uma de cada vez.

modos diferentes

modos diferentes
Isso mostra que haverá 20 sequências diferentes nos modos de se vestir...
Confere aí se bateu o resultado ou se você concorda... Em problemas de contagem é preciso ter cuidado para não deixar as condições impostas de lado e seguir sempre a lógica...
Estou meio que de férias e a mente ta um pouco lenta ainda...
Só os loucos sabem...


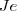 a calça jeans,
a calça jeans, 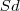 o sapato direito,
o sapato direito,  o sapato esquerdo,
o sapato esquerdo, 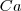 a camisa e
a camisa e 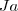 a jaqueta.
a jaqueta.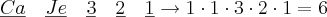 modos diferentes
modos diferentes modos diferentes
modos diferentes modos diferentes
modos diferentes modos diferentes
modos diferentes modos diferentes
modos diferentes

 .
.



