 por gustavoluiss » Qui Set 15, 2011 23:43
por gustavoluiss » Qui Set 15, 2011 23:43
Quantos números maiores que 42815 podem ser formados ...?
Alguém pode me dar um modelo matemático pra questão ?
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Qui Set 15, 2011 23:50
por MarceloFantini » Qui Set 15, 2011 23:50
Não falta um pedaço da questão? "Podem ser formados..."?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gustavoluiss » Qui Set 15, 2011 23:54
por gustavoluiss » Qui Set 15, 2011 23:54
haha esqueçi,ao permutarmos seus algarismos ,,,,
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Sex Set 16, 2011 00:08
por MarceloFantini » Sex Set 16, 2011 00:08
Pense nos casos em que isto é possível: quando a unidade for maior, quando a dezena for maior, quando a centena for maior, quando o milhar for maior e quando a dezena de milhar for maior. Por exemplo, note que permutando os números podemos obter
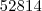
que é maior, ou
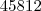
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gustavoluiss » Sex Set 16, 2011 00:11
por gustavoluiss » Sex Set 16, 2011 00:11
eu pensei nisso mais é trabalho ,, queria saber se existiar um modelo mais simples ,,, mais tá ok
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por gustavoluiss » Sex Set 16, 2011 00:18
por gustavoluiss » Sex Set 16, 2011 00:18
Ai achei um número a mais que o gabarito,
2 . 4 . 3 . 2 // podendo começar com 8 ou 5.
dps achei 1 . 2 . 3 . 2 .1 // podendo começar com 4 e ter 8 ou 5 na unidade de milhar.
depois achei 42851 ,,,, oq dá 61.
o gabarito é 60, ajuda ?
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por gvm » Dom Set 18, 2011 12:45
por gvm » Dom Set 18, 2011 12:45
Olá galera, eu estou vendo essa matéria no cursinho agora e tenho tido alguma dificuldade, resolvi entrar nessa seção pra ver alguns exercícios e algumas resoluções, cheguei ao mesmo valor que o gustavoluiss, abaixo eu coloquei a minha resolução passo a passo, se alguém puder dizer onde eu estou errando ou se é erro no gabarito, eu agradeço.
Desde já obrigado.
Eu particularmente adoto um procedimento bem definido pra resolver esse tipo de exercícios, primeiramente eu defino o conjunto dos números que eu posso utilizar, chamando esse conjunto de A, teríamos:
A = {1,2,4,5,8}
Condição: os números devem ser maiores que 42815.
Assim temos:
1º Caso: o algarismo da dezena de milhar é maior que 4.
Nesse caso existem 2 possibilidades de escolha, o 5 e o 8, portanto:
2 x 4 x 3 x 2 x 1 = 48 possibilidades
2º Caso: o algarismo da dezena de milhar é igual a 4.
Nesse caso o algarismo do milhar deve ser maior que 2, uma vez que o 4 já foi escolhido restam o 5 e o 8, portanto:
1 x 2 x 3 x 2 x 1 = 12 possibilidades
3º Caso: o algarismo da dezena de milhar é igual a 4 e o algarismo do milhar é igual a 2.
Nesse caso o algarismo da centena deve ser maior que 8, o que é impossível uma vez que o 8 é o maior número do conjunto A, portanto:
0 possibilidades
4º Caso: o algarismo da dezena de milhar é igual a 4, o algarismo do milhar é igual a 2 e o algarismo da centena é igual a 8.
Nesse caso o algarismo da dezena deve ser maior que 1, logo podemos escolher o número 5, portanto:
1 x 1 x 1 x 1 x 1 = 1 possibilidade (42851)
Somando dá 61.
Pra conferir fiz ao contrário, calculei o total de permutações possíveis e subtrai aquelas que eram menores que 42815, ficou assim:
1º Caso: o algarismo da dezena de milhar é menor que 4.
Nesse caso podemos ter 1 ou 2, portanto:
2 x 4 x 3 x 2 x 1 = 48
2º Caso: o algarismo da dezena de milhar é igual a 4.
Nesse caso o algarismo do milhar deve ser menor que 2, e portanto igual a 1, assim temos:
1 x 1 x 3 x 2 x 1 = 6 possibilidades
3º Caso: o algarismo da dezena de milhar é igual a 4 e o algarismo do milhar é igual a 2.
Nesse caso o algarismo da centena deve ser menor que 8, podendo ser 1 ou 5, portanto:
1 x 1 x 2 x 2 x 1 = 4 possibilidades
4º Caso: o algarismo da dezena de milhar é igual a 4, o algarismo do milhar é igual a 2 e o algarismo da centena é igual a 8.
Nesse caso o algarismo da dezena deve ser menor que 1, o que é impossível, portanto:
0 possibilidades
Somando tudo da 58, mas eu peguei apenas valores menores do que 42815 e não o próprio 42815, portanto eu devo somar 1 ao resultado final, já que o exercício pede apenas valores maiores do que 42815.
E sendo 5! o total de permutações possíveis, temos que o número de valores maiores do que 42815 é dado por 5! - 59 = 61
-
gvm
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Ago 25, 2011 00:02
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando Engenharia
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão do concurso da Compesa-PE - Permutação circular
por Dayse » Qui Fev 21, 2013 18:15
- 5 Respostas
- 3322 Exibições
- Última mensagem por Cleyson007

Sex Fev 22, 2013 09:20
Análise Combinatória
-
- Questão fácil - Certo?
por iceman » Dom Mai 27, 2012 19:57
- 1 Respostas
- 1163 Exibições
- Última mensagem por Russman

Dom Mai 27, 2012 20:07
Números Complexos
-
- Limites - Questão fácil?
por iceman » Dom Set 16, 2012 19:10
- 1 Respostas
- 1472 Exibições
- Última mensagem por DanielFerreira

Dom Set 16, 2012 19:20
Cálculo: Limites, Derivadas e Integrais
-
- [Movimento Curvo] Questão fácil
por gustavoluiss » Ter Ago 23, 2011 14:19
- 10 Respostas
- 5704 Exibições
- Última mensagem por gustavoluiss

Qui Ago 25, 2011 00:11
Álgebra Elementar
-
- [Não sei o nome deste conteúdo] Questão fácil
por tigerwong » Ter Nov 13, 2012 08:52
- 2 Respostas
- 1463 Exibições
- Última mensagem por tigerwong

Ter Nov 13, 2012 15:13
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






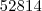 que é maior, ou
que é maior, ou 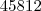 .
.









