 por pogalski » Dom Jun 05, 2011 11:03
por pogalski » Dom Jun 05, 2011 11:03
Estou tentando desenvolver esse exercicio, mas nao consigo chegar a um resultado, nao entendo a fórmula usada.
1. Uma companhia planejou apresentações de vendas para dez clientes importantes. A
probabilidade de receber um pedido como resultado de tal apresentação é estimada em 0,4.
a) Qual é a probabilidade de não receber nenhum pedido como resultado das apresentações?
b) Qual é a probabilidade de todos os dez clientes realizarem pedidos em decorrência da
apresentação realizada?
c) Qual é a probabilidade de receber três ou mais pedidos como resultado das
apresentações?
-
pogalski
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jun 05, 2011 10:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ciências contabeis
- Andamento: cursando
 por Neperiano » Ter Jun 21, 2011 16:34
por Neperiano » Ter Jun 21, 2011 16:34
Ola
Voce tenque usar a probabilidade binomial, se naum souber usar responda q ajudo
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Qua Jun 22, 2011 00:47
por MarceloFantini » Qua Jun 22, 2011 00:47
Vamos denominar por X a quantidade de pedidos como resultado das apresentações. Na item (a), temos:
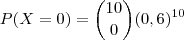
Item (b) é análogo:
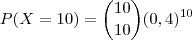
No item (c), temos que pensar um pouco diferente. A probabilidade pedida é
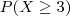
, que é igual a pensar todos os casos menos os que não atendem: quando 2 pedidos são feitos, apenas 1 ou nenhum. Logo:
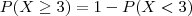
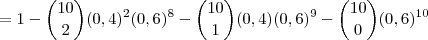
Não domino completamente o assunto, mas acredito que as resoluções sejam assim.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- varíaveis aleatórias contínuas conjuntas
por gprestes » Qua Nov 24, 2010 08:38
- 0 Respostas
- 2541 Exibições
- Última mensagem por gprestes

Qua Nov 24, 2010 08:38
Estatística
-
- Probabilidade-variaveis aleatórias - Help
por benni » Dom Mai 08, 2011 12:03
- 2 Respostas
- 4251 Exibições
- Última mensagem por psdias

Ter Mai 22, 2012 09:42
Probabilidade
-
- [Probablidade] variáveis aleatórias
por 1paulo » Sáb Mai 17, 2014 13:06
- 0 Respostas
- 2227 Exibições
- Última mensagem por 1paulo

Sáb Mai 17, 2014 13:06
Probabilidade
-
- Prova com Variáveis Aleatórias Independentes
 por EREGON » Seg Mai 18, 2015 09:02
por EREGON » Seg Mai 18, 2015 09:02
- 0 Respostas
- 1279 Exibições
- Última mensagem por EREGON

Seg Mai 18, 2015 09:02
Probabilidade
-
- [Variáveis Aleatórias] Esperança Matemática
 por guisore_09 » Ter Dez 29, 2015 08:58
por guisore_09 » Ter Dez 29, 2015 08:58
- 4 Respostas
- 11084 Exibições
- Última mensagem por guisore_09

Dom Jan 03, 2016 10:20
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



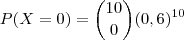
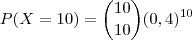
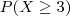 , que é igual a pensar todos os casos menos os que não atendem: quando 2 pedidos são feitos, apenas 1 ou nenhum. Logo:
, que é igual a pensar todos os casos menos os que não atendem: quando 2 pedidos são feitos, apenas 1 ou nenhum. Logo: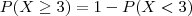
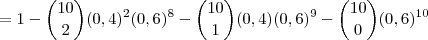


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.