1ª)
![\frac{1}{\sqrt[]{x+\sqrt[]{{x}^{2}-1}}} + \frac{1}{\sqrt[]{x-\sqrt[]{{x}^{2}-1}}} = \sqrt[]{2({x}^{2}+1)} \frac{1}{\sqrt[]{x+\sqrt[]{{x}^{2}-1}}} + \frac{1}{\sqrt[]{x-\sqrt[]{{x}^{2}-1}}} = \sqrt[]{2({x}^{2}+1)}](/latexrender/pictures/6fd065882dbf99bef96077fb0216694a.png)
Eu fiz o mmc e encontrei:
![\frac{\sqrt[]{x-\sqrt[]{{x}^{2}-1}} + \sqrt[]{x+\sqrt[]{{x}^{2}-1}}}{x-\sqrt[]{{x}^{2}-1}} = \frac{x - \sqrt[]{{2x}^{4}-2}}{x-\sqrt[]{{x}^{2}-1}} \frac{\sqrt[]{x-\sqrt[]{{x}^{2}-1}} + \sqrt[]{x+\sqrt[]{{x}^{2}-1}}}{x-\sqrt[]{{x}^{2}-1}} = \frac{x - \sqrt[]{{2x}^{4}-2}}{x-\sqrt[]{{x}^{2}-1}}](/latexrender/pictures/74bc0a3ce986f65d8517abc9a314c907.png)
Elevei ambos os lados ao quadrado e ficou...
![{x-\sqrt[]{{x}^{2}-1} + 2x-2 \sqrt[]{{x}^{2}-1} + {x+\sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} \rightarrow {x-\sqrt[]{{x}^{2}-1} + 2x-2 \sqrt[]{{x}^{2}-1} + {x+\sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} \rightarrow](/latexrender/pictures/02c500a3ce9bb7236d5fd90f0c05d34c.png)
![{2x + 2x-2 \sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} {2x + 2x-2 \sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2}](/latexrender/pictures/2d5ac3e828002fa973385eeb96ce23fd.png)
Daí então não sei mais como fazer... =/
2ª)
![\frac{x + \sqrt[]{3}}{\sqrt[]{x} + \sqrt[]{x+\sqrt[]{3}}} + \frac{x - \sqrt[]{3}}{\sqrt[]{x} - \sqrt[]{x-\sqrt[]{3}}}= \sqrt[]{x} \frac{x + \sqrt[]{3}}{\sqrt[]{x} + \sqrt[]{x+\sqrt[]{3}}} + \frac{x - \sqrt[]{3}}{\sqrt[]{x} - \sqrt[]{x-\sqrt[]{3}}}= \sqrt[]{x}](/latexrender/pictures/75f9d058b62079d440a8acee3695984c.png)
Tirando o mmc encontrei:
![\frac{-x\sqrt[]{x-\sqrt[]{3}} -\sqrt[]{3x - \sqrt[]{3}} + x\sqrt[]{x} + x\sqrt[]{x + \sqrt[]{3}} - \sqrt[]{3x + \sqrt[]{3}} = -\sqrt[]{{x}^{3} - 3x}}{x - \sqrt[]{{x}^{2} - 3}} \frac{-x\sqrt[]{x-\sqrt[]{3}} -\sqrt[]{3x - \sqrt[]{3}} + x\sqrt[]{x} + x\sqrt[]{x + \sqrt[]{3}} - \sqrt[]{3x + \sqrt[]{3}} = -\sqrt[]{{x}^{3} - 3x}}{x - \sqrt[]{{x}^{2} - 3}}](/latexrender/pictures/4e69b1fee8c11edf86498149c8751ad5.png)
nem sei se está certo, mas...
Me ajudem ae por favor...

![\frac{1}{\sqrt[]{x+\sqrt[]{{x}^{2}-1}}} + \frac{1}{\sqrt[]{x-\sqrt[]{{x}^{2}-1}}} = \sqrt[]{2({x}^{2}+1)} \frac{1}{\sqrt[]{x+\sqrt[]{{x}^{2}-1}}} + \frac{1}{\sqrt[]{x-\sqrt[]{{x}^{2}-1}}} = \sqrt[]{2({x}^{2}+1)}](/latexrender/pictures/6fd065882dbf99bef96077fb0216694a.png)
![\frac{\sqrt[]{x-\sqrt[]{{x}^{2}-1}} + \sqrt[]{x+\sqrt[]{{x}^{2}-1}}}{x-\sqrt[]{{x}^{2}-1}} = \frac{x - \sqrt[]{{2x}^{4}-2}}{x-\sqrt[]{{x}^{2}-1}} \frac{\sqrt[]{x-\sqrt[]{{x}^{2}-1}} + \sqrt[]{x+\sqrt[]{{x}^{2}-1}}}{x-\sqrt[]{{x}^{2}-1}} = \frac{x - \sqrt[]{{2x}^{4}-2}}{x-\sqrt[]{{x}^{2}-1}}](/latexrender/pictures/74bc0a3ce986f65d8517abc9a314c907.png)
![{x-\sqrt[]{{x}^{2}-1} + 2x-2 \sqrt[]{{x}^{2}-1} + {x+\sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} \rightarrow {x-\sqrt[]{{x}^{2}-1} + 2x-2 \sqrt[]{{x}^{2}-1} + {x+\sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} \rightarrow](/latexrender/pictures/02c500a3ce9bb7236d5fd90f0c05d34c.png)
![{2x + 2x-2 \sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} {2x + 2x-2 \sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2}](/latexrender/pictures/2d5ac3e828002fa973385eeb96ce23fd.png)
![\frac{x + \sqrt[]{3}}{\sqrt[]{x} + \sqrt[]{x+\sqrt[]{3}}} + \frac{x - \sqrt[]{3}}{\sqrt[]{x} - \sqrt[]{x-\sqrt[]{3}}}= \sqrt[]{x} \frac{x + \sqrt[]{3}}{\sqrt[]{x} + \sqrt[]{x+\sqrt[]{3}}} + \frac{x - \sqrt[]{3}}{\sqrt[]{x} - \sqrt[]{x-\sqrt[]{3}}}= \sqrt[]{x}](/latexrender/pictures/75f9d058b62079d440a8acee3695984c.png)
![\frac{-x\sqrt[]{x-\sqrt[]{3}} -\sqrt[]{3x - \sqrt[]{3}} + x\sqrt[]{x} + x\sqrt[]{x + \sqrt[]{3}} - \sqrt[]{3x + \sqrt[]{3}} = -\sqrt[]{{x}^{3} - 3x}}{x - \sqrt[]{{x}^{2} - 3}} \frac{-x\sqrt[]{x-\sqrt[]{3}} -\sqrt[]{3x - \sqrt[]{3}} + x\sqrt[]{x} + x\sqrt[]{x + \sqrt[]{3}} - \sqrt[]{3x + \sqrt[]{3}} = -\sqrt[]{{x}^{3} - 3x}}{x - \sqrt[]{{x}^{2} - 3}}](/latexrender/pictures/4e69b1fee8c11edf86498149c8751ad5.png)

nathyn escreveu:1ª)
Eu fiz o mmc e encontrei:
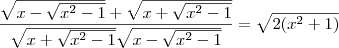
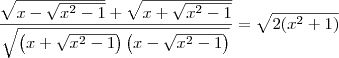
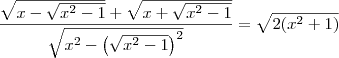
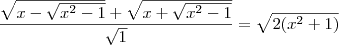
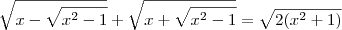
nathyn escreveu:2ª)
Tirando o mmc encontrei:
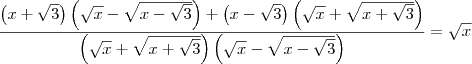
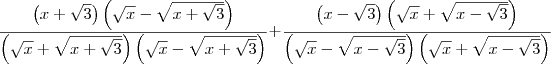
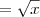
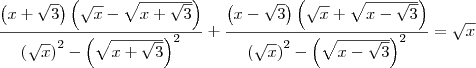
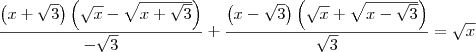


nathyn escreveu:Já a segunda eu não entendi o que foi feito, vc multiplicou em cima e em baica em cada fraçao pela mesma coisa?
nathyn escreveu:Pq foi feito isso e quando eu posso usar esse tipo de simplificação?
nathyn escreveu:Desculpa, é que não tenho uma boa base...


Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante