Já tentei fazer e refazer, mas não faço idéia da resolução.
1)Numa palestra à qual compareceram 420 pessoas, a razão entre o número de homens e mulheres presentes, nes-sa ordem, era igual a 13/8 . Quantos homens assistiram a essa palestra?
(A) 160 (B) 180
(C) 230 (D) 240
(E) 260
Gabarito: E
2)Dentre os maiores parques geradores de energia nuclear, destacam-se os Estados Unidos, a França e o Japão. Juntos, esses três países possuem 218 reatores. Se o número de reatores do Japão dobrasse, este país passaria a ter 6 reatores a mais que os Estados Unidos. Sabe-se, também, que na França há 4 reatores a mais do que no Japão. Qual é a diferença entre o número de reatores dos Estados Unidos e da França?
(A) 45 (B) 49
(C) 55 (D) 59
(E) 65
Gabarito: A


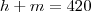
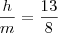
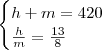
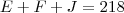
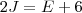
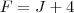
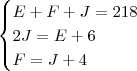

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)