Brother tentei fazer por sistema mas ñ conseguie tentei fazer por essa formula aqui
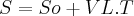 e tbm ñ me ajuda aew nessa questão desde já agradecido...
e tbm ñ me ajuda aew nessa questão desde já agradecido...
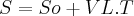 e tbm ñ me ajuda aew nessa questão desde já agradecido...
e tbm ñ me ajuda aew nessa questão desde já agradecido...



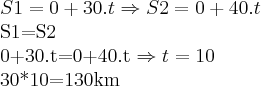

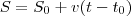 , pois isso conta o instante inicial onde o móvel sai. No primeiro caso,
, pois isso conta o instante inicial onde o móvel sai. No primeiro caso,  mas no segundo
mas no segundo  . Note que sua igualdade não faz sentido:
. Note que sua igualdade não faz sentido:  só acontece se
só acontece se  , que também não é uma resposta válida. Vamos montar o problema:
, que também não é uma resposta válida. Vamos montar o problema: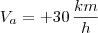 . Assim, a velocidade do segundo trem será no sentido oposto, e portanto terá sinal oposto:
. Assim, a velocidade do segundo trem será no sentido oposto, e portanto terá sinal oposto: 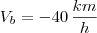 . Adotando como origem a cidade A, o espaço inicial do primeiro trem é zero e do segundo trem é 200 km. Vamos equacionar:
. Adotando como origem a cidade A, o espaço inicial do primeiro trem é zero e do segundo trem é 200 km. Vamos equacionar: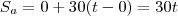
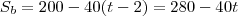
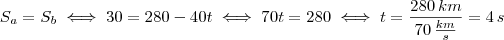
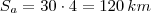


Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.