 por umaiafilho » Sex Mai 13, 2011 09:02
por umaiafilho » Sex Mai 13, 2011 09:02
Resolver esta equação:
Encontrei um resultado x= 3/6

-
umaiafilho
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qui Mai 12, 2011 20:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CONTABEIS
- Andamento: cursando
 por carlosalesouza » Sex Mai 13, 2011 09:18
por carlosalesouza » Sex Mai 13, 2011 09:18
Bem simples... rs
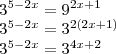
Note que, se em ambos os lados temos a mesma base elevada a expoentes "diferentes" e o resultado de ambas as potências é igual, logo os expoentes são iguais...
Um erro muito comum quando se está aprendendo equação exponencial, é achar que nós vamos "cortar" as bases... isso é uma ideia falsa... na verdade, nada se corta, nem se passa para "o outro lado"... os valores realizam operações entre si e, se sabemos que podemos modificar ambos os lados da igualdade da mesma forma a igualdade se mantém, então usamos a simetria para eliminar um valor em um lado, transferindo-o para outro...
Agora, chega de verborragia, sabemos, como dito acima, que:
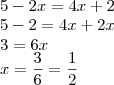
Viu? sua resposta estava certa.... o único detalhe, é que é interessante simplificarmos o resultado ao máximo, para obtermos uma resposta mais enchuta... fica difícil, às vezes, notar coisas do tipo:
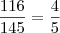
só de bater o olho...rs ... certo?
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por umaiafilho » Sex Mai 13, 2011 09:24
por umaiafilho » Sex Mai 13, 2011 09:24
Obrigado!
Valeu pela dica!
-
umaiafilho
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qui Mai 12, 2011 20:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CONTABEIS
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (AFA) equação exponenciais
por natanskt » Sex Out 08, 2010 20:05
- 3 Respostas
- 2111 Exibições
- Última mensagem por Molina

Sex Out 08, 2010 22:19
Funções
-
- Equação Exponenciais
por umaiafilho » Qui Mai 12, 2011 21:35
- 2 Respostas
- 1275 Exibições
- Última mensagem por umaiafilho

Qui Mai 12, 2011 23:02
Sistemas de Equações
-
- Equação Exponenciais
por umaiafilho » Sáb Mai 14, 2011 11:50
- 2 Respostas
- 1271 Exibições
- Última mensagem por umaiafilho

Sáb Mai 14, 2011 14:16
Sistemas de Equações
-
- Equação Exponenciais
por umaiafilho » Sáb Mai 14, 2011 17:12
- 4 Respostas
- 1962 Exibições
- Última mensagem por umaiafilho

Sáb Mai 14, 2011 20:09
Sistemas de Equações
-
- Exponenciais
por Souo » Ter Jun 30, 2015 01:42
- 3 Respostas
- 2702 Exibições
- Última mensagem por nakagumahissao

Sex Jul 03, 2015 21:24
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




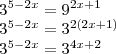
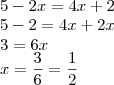
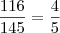 só de bater o olho...rs ... certo?
só de bater o olho...rs ... certo?
