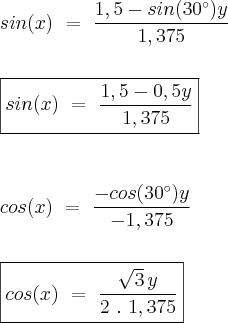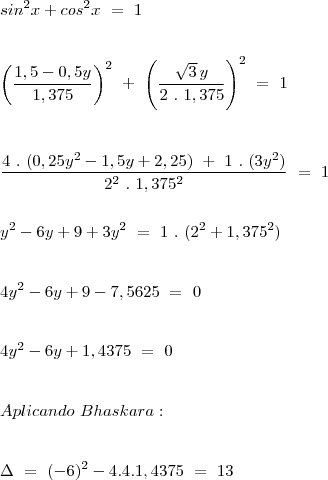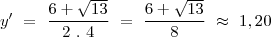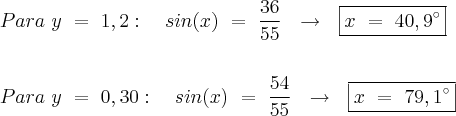-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478908 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 536714 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 500442 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 719963 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2146788 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Therodrigou » Seg Mar 25, 2019 04:00
por Therodrigou » Seg Mar 25, 2019 04:00
Olá, gostaria de pedir ajuda para resolver esse sistema:
1,375*sin(x) + sin(30)*y - 1,5 = 0
- 1,375*cos(x) + cos(30)*y = 0
Resposta:
y = 1,2
x = 40,9
Esse sistema tem solução, foi retirado de uma questão de física, apenas troquei as variáveis para facilitar, conforme a imagem:
https://image.slidesharecdn.com/chapter ... 1510090397
-
Therodrigou
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Jun 20, 2018 06:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia mecânica
- Andamento: cursando
 por Gebe » Seg Mar 25, 2019 15:54
por Gebe » Seg Mar 25, 2019 15:54
Vamos começar
isolando sin(x) e cos(x) na 1ª e 2ª equação respectivamente:
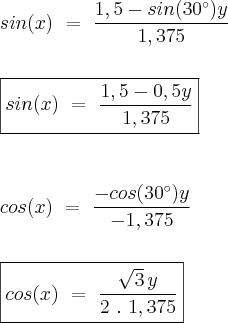 Agora aplicando a identidade sin²x + cos²x = 1
Agora aplicando a identidade sin²x + cos²x = 1:
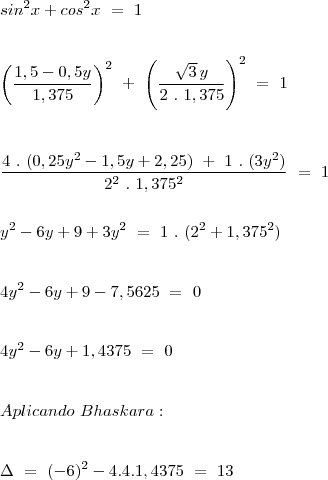
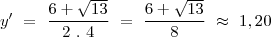

Substituindo os valores de "y" nas equações acharemos:
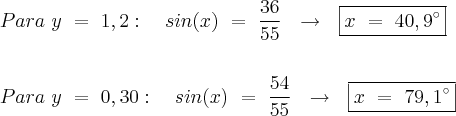 Obs.: Não consegui identificar no problema se há alguma condição que recuse o par (x,y) = (79,1° , 0,30) como solução
Obs.: Não consegui identificar no problema se há alguma condição que recuse o par (x,y) = (79,1° , 0,30) como solução
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por Therodrigou » Seg Mar 25, 2019 18:40
por Therodrigou » Seg Mar 25, 2019 18:40
Obrigado! O y seria o valor de uma força, apenas o x seria o ângulo!
-
Therodrigou
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Jun 20, 2018 06:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia mecânica
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Seno e Cosseno de X??
por Leone de Paula » Ter Jul 13, 2010 00:28
- 1 Respostas
- 4250 Exibições
- Última mensagem por Tom

Ter Jul 13, 2010 00:43
Geometria Plana
-
- Lei do seno e cosseno
 por renataf » Sex Dez 03, 2010 11:06
por renataf » Sex Dez 03, 2010 11:06
- 7 Respostas
- 17878 Exibições
- Última mensagem por Lorettto

Sáb Dez 11, 2010 01:17
Trigonometria
-
- Seno e Cosseno
por karen » Qua Mai 16, 2012 22:20
- 1 Respostas
- 3438 Exibições
- Última mensagem por joaofonseca

Qui Mai 17, 2012 08:51
Trigonometria
-
- Seno e Cosseno
por Malorientado » Sáb Ago 18, 2012 17:55
- 1 Respostas
- 2479 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 18, 2012 19:33
Trigonometria
-
- Seno e Cosseno
por Malorientado » Sáb Ago 18, 2012 18:12
- 1 Respostas
- 1568 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 18, 2012 19:33
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 26 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.