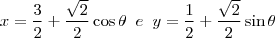-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477821 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529195 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 492751 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 698208 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2108091 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por T0LKIEN » Ter Mar 29, 2016 11:20
por T0LKIEN » Ter Mar 29, 2016 11:20
2x^2 + 2y^2 - 6x - 2y + 4 = 0
-
T0LKIEN
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 29, 2016 11:11
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia
- Andamento: cursando
 por nakagumahissao » Sáb Mai 07, 2016 23:18
por nakagumahissao » Sáb Mai 07, 2016 23:18
Primeiramente precisamos completar os quadrados para obtermos uma equação mais "simplificada", que neste caso é a de um círcunferência:
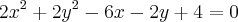
Dividindo-se os dois lados desta equação por 2 teremos:
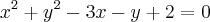
Reordenando...

Completando-se os quadrados:
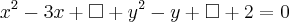
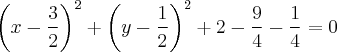
Logo,
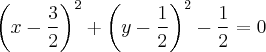
![{\left(x - \frac{3}{2} \right)}^{2} + {\left(y - \frac{1}{2} \right)}^{2} = \frac{1}{2} \;\;\;\;\;\;[1] {\left(x - \frac{3}{2} \right)}^{2} + {\left(y - \frac{1}{2} \right)}^{2} = \frac{1}{2} \;\;\;\;\;\;[1]](/latexrender/pictures/cd7078eb35a7a54024dd442e0e77e603.png)
que se trata de uma circunferência com centro em (3/2, 1/2) e raio

Se queremos parametrizar esta curva, podemos fazer, utilizando o centro (3/2, 1/2):
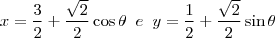
Que é a parametrização procurada.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função da curva S] Qual é Função desta curva?
por Joao Petrocelle » Qua Nov 14, 2012 14:45
- 7 Respostas
- 3796 Exibições
- Última mensagem por young_jedi

Qua Nov 14, 2012 21:19
Funções
-
- Comprimento de curva
por dsbonafe » Ter Out 13, 2009 16:39
- 1 Respostas
- 2374 Exibições
- Última mensagem por Camolas

Sex Mai 31, 2013 15:27
Cálculo: Limites, Derivadas e Integrais
-
- Curva borboleta
 por LuizAquino » Sáb Jul 30, 2011 13:51
por LuizAquino » Sáb Jul 30, 2011 13:51
- 1 Respostas
- 1863 Exibições
- Última mensagem por Neperiano

Sáb Ago 20, 2011 22:39
Assuntos Gerais ou OFF-TOPIC
-
- Comprimento da curva
por Crist » Qui Nov 29, 2012 13:32
- 6 Respostas
- 3152 Exibições
- Última mensagem por young_jedi

Ter Dez 11, 2012 11:01
Cálculo: Limites, Derivadas e Integrais
-
- Comprimento de Curva
por Marcossiva » Sex Jun 28, 2013 10:59
- 3 Respostas
- 1801 Exibições
- Última mensagem por Marcossiva

Sex Jun 28, 2013 11:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



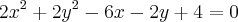
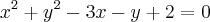

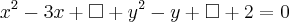
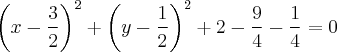
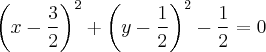
![{\left(x - \frac{3}{2} \right)}^{2} + {\left(y - \frac{1}{2} \right)}^{2} = \frac{1}{2} \;\;\;\;\;\;[1] {\left(x - \frac{3}{2} \right)}^{2} + {\left(y - \frac{1}{2} \right)}^{2} = \frac{1}{2} \;\;\;\;\;\;[1]](/latexrender/pictures/cd7078eb35a7a54024dd442e0e77e603.png)