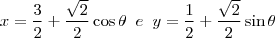Primeiramente precisamos completar os quadrados para obtermos uma equação mais "simplificada", que neste caso é a de um círcunferência:
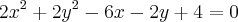
Dividindo-se os dois lados desta equação por 2 teremos:
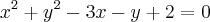
Reordenando...

Completando-se os quadrados:
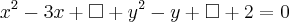
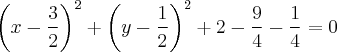
Logo,
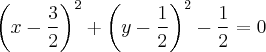
![{\left(x - \frac{3}{2} \right)}^{2} + {\left(y - \frac{1}{2} \right)}^{2} = \frac{1}{2} \;\;\;\;\;\;[1] {\left(x - \frac{3}{2} \right)}^{2} + {\left(y - \frac{1}{2} \right)}^{2} = \frac{1}{2} \;\;\;\;\;\;[1]](/latexrender/pictures/cd7078eb35a7a54024dd442e0e77e603.png)
que se trata de uma circunferência com centro em (3/2, 1/2) e raio

Se queremos parametrizar esta curva, podemos fazer, utilizando o centro (3/2, 1/2):
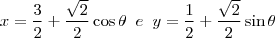
Que é a parametrização procurada.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali



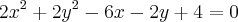
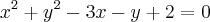

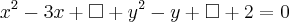
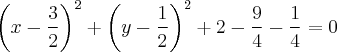
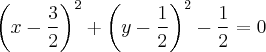
![{\left(x - \frac{3}{2} \right)}^{2} + {\left(y - \frac{1}{2} \right)}^{2} = \frac{1}{2} \;\;\;\;\;\;[1] {\left(x - \frac{3}{2} \right)}^{2} + {\left(y - \frac{1}{2} \right)}^{2} = \frac{1}{2} \;\;\;\;\;\;[1]](/latexrender/pictures/cd7078eb35a7a54024dd442e0e77e603.png)