Sistema linear
Boa tarde galera! Enrosquei em um sisteminha...
Seja o sistema
x + y + z= 0
-x + (sen )y + 2z =0 No enunciado essa equação veio sem igualdade, por isso considerei sendo =0
)y + 2z =0 No enunciado essa equação veio sem igualdade, por isso considerei sendo =0
x + (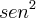
 )y + 4z = 0
)y + 4z = 0
sendo um número real no intervalo [0,2
um número real no intervalo [0,2 ].
].
a) Determine para que o sistema tenha infinitas soluções
para que o sistema tenha infinitas soluções
b) Para o valor de encontrado no item a, resolva o sistema.
encontrado no item a, resolva o sistema.
Resposta: a) 3 /2 b)S={(-
/2 b)S={(- ,
,  , 0),
, 0), 
 }.
}.
Eu cheguei em dois resultado para o sen: -2 e 3.
Obg!
Obs: me desculpem, mas não consegui colocar a fórmula no LaTeX, sempre dava algum erro...
Seja o sistema
x + y + z= 0
-x + (sen
 )y + 2z =0 No enunciado essa equação veio sem igualdade, por isso considerei sendo =0
)y + 2z =0 No enunciado essa equação veio sem igualdade, por isso considerei sendo =0x + (
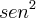
 )y + 4z = 0
)y + 4z = 0sendo
 um número real no intervalo [0,2
um número real no intervalo [0,2 ].
].a) Determine
 para que o sistema tenha infinitas soluções
para que o sistema tenha infinitas soluçõesb) Para o valor de
 encontrado no item a, resolva o sistema.
encontrado no item a, resolva o sistema.Resposta: a) 3
 /2 b)S={(-
/2 b)S={(- ,
,  , 0),
, 0), 
 }.
}.Eu cheguei em dois resultado para o sen: -2 e 3.
Obg!
Obs: me desculpem, mas não consegui colocar a fórmula no LaTeX, sempre dava algum erro...
 , uma vez que
, uma vez que 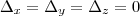 (sistema homogêneo).
(sistema homogêneo).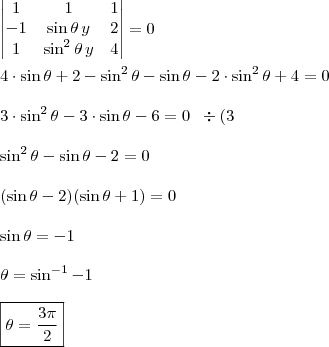
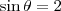 pois
pois  .
. .
.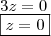 .
.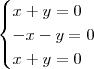 . Como podemos notar, as três equação são proporcionais; com efeito,
. Como podemos notar, as três equação são proporcionais; com efeito,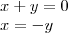
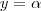 , concluímos que
, concluímos que 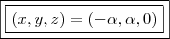 !!
!!