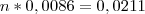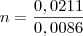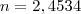por nicecaps » Ter Mar 30, 2010 12:22
por nicecaps » Ter Mar 30, 2010 12:22
Determine o valor de "n" na expressão: n . log 1,02 = log 1,05
O professor resolveu assim assim:
n . log 1,02 = log 1,05
n=0,1761 / 0,0086
n= 20,47
Não consegui entender muito bem, peço por favor que me expliquem detalhadamente
-
nicecaps
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Out 26, 2009 11:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Contábeis
- Andamento: cursando
 por Molina » Ter Mar 30, 2010 13:38
por Molina » Ter Mar 30, 2010 13:38
nicecaps escreveu:Determine o valor de "n" na expressão: n . log 1,02 = log 1,05
O professor resolveu assim assim:
n . log 1,02 = log 1,05
n=0,1761 / 0,0086
n= 20,47
Não consegui entender muito bem, peço por favor que me expliquem detalhadamente
Bom dia.
Isso nada mais é do que uma equação. os
logs nada mais são do que números reais e o
n é a incognita.
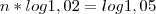
Usando uma calculadora para descobrir o valor de

e de
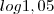
, chegamos em
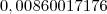
e
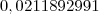
, respectivamente. O que o professor fez foi usar apenas quatro casas decimais. O valor do segundo log do seu professor deu diferente do meu. Fiz usando a calculadora do Google e você pode comprovar isso
clicando aqui. Continuando...
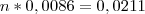
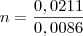
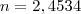
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por nicecaps » Qua Mar 31, 2010 15:29
por nicecaps » Qua Mar 31, 2010 15:29
Molina,
muto obrigada mesmo. Agora consegui entender...
-
nicecaps
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Out 26, 2009 11:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Contábeis
- Andamento: cursando
Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



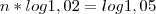
 e de
e de 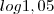 , chegamos em
, chegamos em 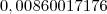 e
e 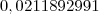 , respectivamente. O que o professor fez foi usar apenas quatro casas decimais. O valor do segundo log do seu professor deu diferente do meu. Fiz usando a calculadora do Google e você pode comprovar isso clicando aqui. Continuando...
, respectivamente. O que o professor fez foi usar apenas quatro casas decimais. O valor do segundo log do seu professor deu diferente do meu. Fiz usando a calculadora do Google e você pode comprovar isso clicando aqui. Continuando...