-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478845 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 536066 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 499723 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 718051 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2143158 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por juliosellsman » Qua Jun 03, 2015 21:55
por juliosellsman » Qua Jun 03, 2015 21:55
Boa noite.
Me ajude, por favor.
Estou com dificuldades em resolver o sistema abaixo e discutir?
Ele é compatível? Se compatível, determinado ou indeterminado? ou Impossível?
Desculpe por não postar na linguagem LaTex.
x + 2y = -4
-3x + 4y = -18
2x -y=7
Tentei resolver por escalonamento e resultou na seguinte forma reduzida ampliada:
1 2 -4
0 1 -3
0 0 0
Porém, Pa =3 e Pc=2, seria impossível.
Mas, como a última linha é nula, deveria ser compatível indeterminado. Porém, logo percebe-se na segunda linha que y=-3. substituindo na 1ª equação x = 2.
Esses valores de x=2 e y=-3, atende todas as equações, então, o sistema é determinado e o conjunto solução é S = {2, -3}
Preciso de uma ajuda, estou me questionando o que fiz de errado para ter tanta dúvida neta resposta.
Desde já agradeço,
Julio C.
-
juliosellsman
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jun 03, 2015 21:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por DanielFerreira » Qui Jun 04, 2015 23:18
por DanielFerreira » Qui Jun 04, 2015 23:18
Olá
Julio, boa noite!
Note que ao somar todas as equações do sistema, somos capazes de encontrar uma das variáveis, veja:
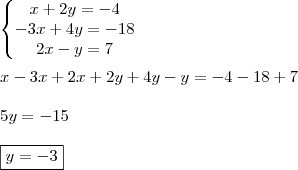
Conclusão, tua resposta está correcta!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por juliosellsman » Sex Jun 05, 2015 00:14
por juliosellsman » Sex Jun 05, 2015 00:14
Muito obrigado.
Porém, vc pode continuar me ajudando? Estou tentando entender por que após escalonar a última linha foi nula. Se é um SPD, a última linha pode ser nula?
-
juliosellsman
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jun 03, 2015 21:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por DanielFerreira » Dom Jun 07, 2015 10:45
por DanielFerreira » Dom Jun 07, 2015 10:45
Acho que entendi sua dúvida: você está achando que o sistema é indeterminado, é isso? Se for, a resposta é não; o sistema é DETERMINADO.
Se tivéssemos diante de um sistema com três variáveis, por exemplo, e uma das linhas fosse anulada após o escalonamento, aí sim o sistema seria indeterminado. No seu exercício, temos apenas duas variáveis.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por juliosellsman » Dom Jun 07, 2015 13:43
por juliosellsman » Dom Jun 07, 2015 13:43
Obrigado. Era isso mesmo. Alguns autores não deixam claro que apenas sistemas quadrados, ao escalonar, se restar a última linha zerada, ele é indeterminado. Infelizmente, eles generaliza.
-
juliosellsman
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jun 03, 2015 21:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 2629 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Sistema linear] Sistema linear com constante
por smlspirit » Qui Jul 19, 2012 19:34
- 4 Respostas
- 4842 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 22:40
Sistemas de Equações
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4034 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema linear
por kael » Ter Out 20, 2009 14:14
- 1 Respostas
- 2350 Exibições
- Última mensagem por kael

Ter Out 20, 2009 16:24
Sistemas de Equações
-
- Sistema Linear
por kael » Qua Out 21, 2009 13:43
- 1 Respostas
- 3292 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2009 15:26
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 24 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


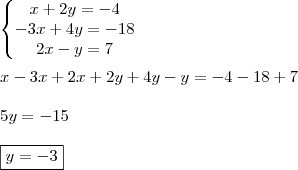

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.