 por juliosellsman » Qua Jun 03, 2015 21:55
por juliosellsman » Qua Jun 03, 2015 21:55
Boa noite.
Me ajude, por favor.
Estou com dificuldades em resolver o sistema abaixo e discutir?
Ele é compatível? Se compatível, determinado ou indeterminado? ou Impossível?
Desculpe por não postar na linguagem LaTex.
x + 2y = -4
-3x + 4y = -18
2x -y=7
Tentei resolver por escalonamento e resultou na seguinte forma reduzida ampliada:
1 2 -4
0 1 -3
0 0 0
Porém, Pa =3 e Pc=2, seria impossível.
Mas, como a última linha é nula, deveria ser compatível indeterminado. Porém, logo percebe-se na segunda linha que y=-3. substituindo na 1ª equação x = 2.
Esses valores de x=2 e y=-3, atende todas as equações, então, o sistema é determinado e o conjunto solução é S = {2, -3}
Preciso de uma ajuda, estou me questionando o que fiz de errado para ter tanta dúvida neta resposta.
Desde já agradeço,
Julio C.
-
juliosellsman
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jun 03, 2015 21:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por DanielFerreira » Qui Jun 04, 2015 23:18
por DanielFerreira » Qui Jun 04, 2015 23:18
Olá
Julio, boa noite!
Note que ao somar todas as equações do sistema, somos capazes de encontrar uma das variáveis, veja:
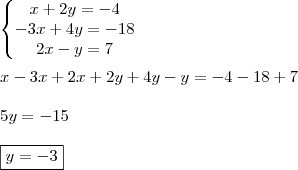
Conclusão, tua resposta está correcta!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por juliosellsman » Sex Jun 05, 2015 00:14
por juliosellsman » Sex Jun 05, 2015 00:14
Muito obrigado.
Porém, vc pode continuar me ajudando? Estou tentando entender por que após escalonar a última linha foi nula. Se é um SPD, a última linha pode ser nula?
-
juliosellsman
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jun 03, 2015 21:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por DanielFerreira » Dom Jun 07, 2015 10:45
por DanielFerreira » Dom Jun 07, 2015 10:45
Acho que entendi sua dúvida: você está achando que o sistema é indeterminado, é isso? Se for, a resposta é não; o sistema é DETERMINADO.
Se tivéssemos diante de um sistema com três variáveis, por exemplo, e uma das linhas fosse anulada após o escalonamento, aí sim o sistema seria indeterminado. No seu exercício, temos apenas duas variáveis.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por juliosellsman » Dom Jun 07, 2015 13:43
por juliosellsman » Dom Jun 07, 2015 13:43
Obrigado. Era isso mesmo. Alguns autores não deixam claro que apenas sistemas quadrados, ao escalonar, se restar a última linha zerada, ele é indeterminado. Infelizmente, eles generaliza.
-
juliosellsman
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Jun 03, 2015 21:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3091 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Sistema linear] Sistema linear com constante
por smlspirit » Qui Jul 19, 2012 19:34
- 4 Respostas
- 5555 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 22:40
Sistemas de Equações
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4496 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema linear
por kael » Ter Out 20, 2009 14:14
- 1 Respostas
- 2671 Exibições
- Última mensagem por kael

Ter Out 20, 2009 16:24
Sistemas de Equações
-
- Sistema Linear
por kael » Qua Out 21, 2009 13:43
- 1 Respostas
- 3637 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2009 15:26
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


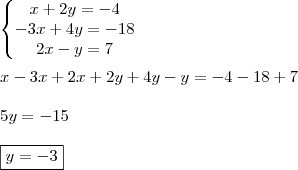

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
