-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480122 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 538720 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 502567 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 725118 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2160226 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por marcel felipe » Sáb Mai 23, 2015 15:31
por marcel felipe » Sáb Mai 23, 2015 15:31
Um presente de casamento, cujo valor era R$ 900,00, deveria ser comprado por um grupo de pessoas que contribuiriam
com quantias iguais. Como três delas desistiram da compra, a quota de cada um dos outros ficou aumentada
em R$ 15,00. O número de pessoas que compraram o presente foi
a) 12
b) 15
c) 60
d) 9
resposta e 12
eu pensei o seguite
x > numero de pessoas
v > valor de cada contribuiçao
xv = 900
depois das 3 pessoas que sairam e do acrescimo de 15 reais as restantes
(x-3)(v+15)=900
sistema
xv = 900
(x-3)(v+15)=900
eu nao estou conseguindo resolver esse sistema, por favor me ajudem.
obrigado.
-
marcel felipe
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 28, 2012 15:56
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Sáb Mai 23, 2015 18:47
por Cleyson007 » Sáb Mai 23, 2015 18:47
Boa noite Marcel!
Eu nem cheguei a olhar como você montou o sistema. Como a sua dúvida está em resolvê-lo, vamos lá:
Você tem que encontrar o valor de "x"!
Isolando "v" na primeira equação:
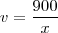
Substitua esse valor que encontramos para "v" na segunda equação. Em outras palavras, resolva a equação:
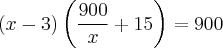
Consegue sozinho?
Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por marcel felipe » Sáb Mai 23, 2015 23:09
por marcel felipe » Sáb Mai 23, 2015 23:09
consegui resolver obrigado
-
marcel felipe
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Abr 28, 2012 15:56
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Uma questa da FMABC
por JuHs2Jow » Qua Nov 30, 2011 15:10
- 1 Respostas
- 2131 Exibições
- Última mensagem por DanielFerreira

Sex Dez 16, 2011 21:08
Sistemas de Equações
-
- [Equações Diferenciais] Dúvida com exercício simples
por Leonardo Ribeiro » Sáb Mar 07, 2015 01:28
- 2 Respostas
- 1540 Exibições
- Última mensagem por Leonardo Ribeiro

Sáb Mar 07, 2015 11:58
Cálculo: Limites, Derivadas e Integrais
-
- [Equações] Me ajudem nessas equações do meu trabalho!
por henriquea92 » Sáb Jun 01, 2013 15:53
- 0 Respostas
- 2699 Exibições
- Última mensagem por henriquea92

Sáb Jun 01, 2013 15:53
Equações
-
- [Equações] Determinar Frações de equações
por fenixxx » Ter Fev 28, 2012 21:28
- 2 Respostas
- 3600 Exibições
- Última mensagem por fenixxx

Qua Fev 29, 2012 17:08
Funções
-
- Equações cartesianas e equações paramétricas
por Victor Mello » Sáb Ago 23, 2014 16:24
- 1 Respostas
- 2939 Exibições
- Última mensagem por Russman

Sáb Ago 23, 2014 18:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.