 por brunotst » Dom Ago 29, 2010 11:41
por brunotst » Dom Ago 29, 2010 11:41
Galera não estou conseguindo resolver o problema abaixo, consigo encontrar meus resultados mas não bate com nenhuma resposta, chego a R$2.812,50 para o primeiro e terceiro funcionário, e R$1.406,25 para o segundo funcionário. Me ajudem.
Um prêmio de 5.625,00 será distribuido entre três funcionários de uma empresa na razão direta do tempo de trabalho nesta empresa, e na razão inversa na média anual de faltas de cada um. O primeiro(mais antigo) que trabalha a 8 anos na empresa, faltou 8 vezes; o segundo, que está lá a 5 anos, faltou 10 vezes; o terceiro está a apenas 1,5 ano e faltou 3 vezes. Qual será o valor a que tem direito aquele que irá receber mais?
a)R$4.000,00
b)R$3.600,00
c)R$2.500,00
d)R$1.900,00
e)R$1.800,00
-
brunotst
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Ago 01, 2010 12:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por brunotst » Seg Ago 30, 2010 21:17
por brunotst » Seg Ago 30, 2010 21:17
Não entendi Fantini.
-
brunotst
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Ago 01, 2010 12:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por MarceloFantini » Seg Ago 30, 2010 23:29
por MarceloFantini » Seg Ago 30, 2010 23:29
A divisão será feita entre três funcionários. A parte que cada um receberá é proporcional ao tempo de trabalho (

) e proporcional ao inverso de faltas no período todo (
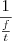
).
Então:
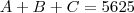
, onde:
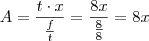
,
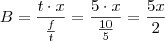
e
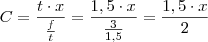
. Jogando de volta na equação você tem o que eu postei antes.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problemas do Prêmio Milenium
por Neperiano » Sex Mai 07, 2010 19:12
- 3 Respostas
- 4401 Exibições
- Última mensagem por Neperiano

Sáb Mai 08, 2010 16:02
Mensagens Matemáticas
-
- Divisão por Zero
por harumitu » Qui Mar 29, 2012 07:07
- 1 Respostas
- 3405 Exibições
- Última mensagem por MarceloFantini

Qui Mar 29, 2012 10:47
Álgebra Elementar
-
- Divisão
por alvessp » Qui Ago 21, 2014 04:17
- 1 Respostas
- 2576 Exibições
- Última mensagem por Russman

Sex Ago 22, 2014 22:16
Cálculo: Limites, Derivadas e Integrais
-
- Divisão
por antonybel » Seg Dez 09, 2019 17:32
- 1 Respostas
- 6202 Exibições
- Última mensagem por adauto martins

Qui Dez 12, 2019 13:47
Aritmética
-
- [divisão] Ajuda, plz!
por Roberta » Ter Jun 24, 2008 13:25
- 2 Respostas
- 2751 Exibições
- Última mensagem por Roberta

Ter Jun 24, 2008 14:45
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




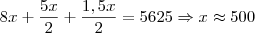
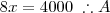


 ) e proporcional ao inverso de faltas no período todo (
) e proporcional ao inverso de faltas no período todo (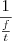 ).
).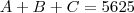 , onde:
, onde: 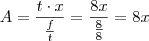 ,
, 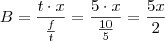 e
e 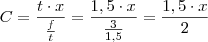 . Jogando de volta na equação você tem o que eu postei antes.
. Jogando de volta na equação você tem o que eu postei antes. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.