Olá Fernanda!!! Vamos tentar resolver esse seu problema (agora virou nosso... kkkkkkkkk)

!
O método de escalonamento consiste em escalonar a sua equação; mais basicamente transformar seu sistema numa escada. Depois de transformá-lo, você verá o quão fácil é determinar a solução dele (na verdade, você escalona seu sistema com o intuito de determinar as soluções do mesmo!). Bem, chega de conversa. Cálculos:
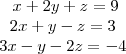
O primeiro passo é anular o termo que contém a incógnita x da segunda equação. Para tanto, vamos usar a primeira equação. Multiplicando a primeira equação por
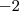
e some com a segunda equação. Fazendo assim teremos o sistema:
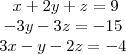
Esse sistema é equivalente ao primeiro. Chamamos de equivalente e não de igual porque há uma mudança dos termos. É equivalente porque a solução desse novo sistema é a mesma solução do sistema anterior. Você não faz o curso de matemática né???? Mas isso não te impede de saber de equivalência. Procure um professor de matemática da faculdade mais próxima e pergunte a ele... Isso já está virando comercial...

Continuando...
O próximo passo é semelhante ao primeiro só que vamos anular o termo que contém a incógnita x na terceira equação. Multiplicando a primeira equação por
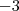
e some com a terceira equação:
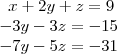
Podemos simplificar a segunda equação dividindo-a por
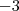
, certo? :
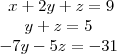
O próximo passo é anular o termo que contém incógnita y da terceira equação, utilizando a segunda equação (repare que, se usarmos a primeira equação, o termo que contém a incógnita x retorna e não queremos isso. Não, você não quer isso! rsrsrssrsr). Multiplicando a segunda equação por
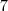
e somando com a terceira, temos:
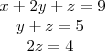
Pronto! Seu sistema está escalonado! Se você organizar em seu caderno esse sistema, termos de mesma incógnita em cima de termos de mesma incógnita, verá uma escada, ou não.kkkkkkkk
Agora, se você quiser solucionar o seu sistema, basta "subir a sua escada". Da terceira equação temos:
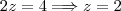
Substituindo esse resultado na segunda equação temos:
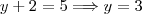
Substituindo esses dois valores encontrados na 1ª equação, temos:
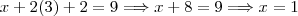
Logo, você tem a solução do seu sistema:
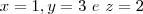
.
Observações:
_Qualquer dúvida, por favor, AVISE!!!!!!!!!!!!!!!!!!!
_Qualquer erro também!!!!!!!!



 !
!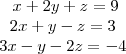
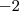 e some com a segunda equação. Fazendo assim teremos o sistema:
e some com a segunda equação. Fazendo assim teremos o sistema: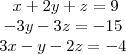
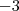 e some com a terceira equação:
e some com a terceira equação: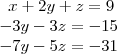
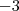 , certo? :
, certo? :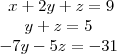
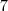 e somando com a terceira, temos:
e somando com a terceira, temos: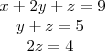
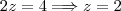
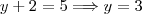
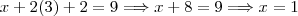
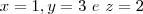 .
.




![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)