-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 479997 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 537815 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 501554 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 722444 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2155871 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por matemarcos » Qui Jan 11, 2018 22:26
por matemarcos » Qui Jan 11, 2018 22:26
Um grupo de amigos reuniu-se, em uma pizzaria, para um jantar de confraternização de fim de ano. Após receber a conta, verificaram que, se cada um contribuísse com R$ 15,00 ainda faltariam R$ 50,00 para pagar a conta. Se cada um contribuísse com R$ 23,00, sobrariam R$ 14,00. Dessa forma, conclui-se que o grupo era composto de
A) 8 pessoas. C) 6 pessoas.
B) 7 pessoas. D) 9 pessoas
-
matemarcos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Jan 11, 2018 22:09
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Informática
- Andamento: formado
 por DanielFerreira » Qui Jan 25, 2018 11:43
por DanielFerreira » Qui Jan 25, 2018 11:43
Olá
matemarcos, seja bem-vindo!
matemarcos escreveu:Um grupo de amigos reuniu-se, em uma pizzaria, para um jantar de confraternização de fim de ano. Após receber a conta, verificaram que, se cada um contribuísse com R$ 15,00 ainda faltariam R$ 50,00 para pagar a conta. Se cada um contribuísse com R$ 23,00, sobrariam R$ 14,00. Dessa forma, conclui-se que o grupo era composto de
A) 8 pessoas. C) 6 pessoas.
B) 7 pessoas. D) 9 pessoas
Seja

a quantidade de pessoas do grupo de amigos e

a quantia gasta por eles. De acordo com o enunciado,
CONDIÇÃO I:
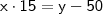 CONDIÇÃO II
CONDIÇÃO II:
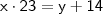
Ora, resolvendo sistema formado pelas duas equações acima...

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como resolver esta indeterminação?
por joaofonseca » Qui Mar 22, 2012 14:57
- 2 Respostas
- 2914 Exibições
- Última mensagem por joaofonseca

Qui Mar 22, 2012 18:37
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver esta Formula
por ana maria » Ter Dez 17, 2013 11:57
- 6 Respostas
- 3516 Exibições
- Última mensagem por ana maria

Ter Dez 17, 2013 15:26
Matemática Financeira
-
- [Inequeções] Como resolver esta?
por alienante » Seg Dez 30, 2013 10:18
- 2 Respostas
- 1933 Exibições
- Última mensagem por Renato_RJ

Seg Dez 30, 2013 14:27
Álgebra Elementar
-
- Logarítmos - Como resolver esta expressão
por petras » Qui Out 20, 2016 10:35
- 3 Respostas
- 7438 Exibições
- Última mensagem por DanielFerreira

Seg Out 24, 2016 22:08
Logaritmos
-
- Não consigo resolver esta questão.
por marianacarvalhops » Sex Mai 15, 2009 21:10
- 2 Respostas
- 2232 Exibições
- Última mensagem por admin

Sáb Mai 16, 2009 21:12
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 a quantidade de pessoas do grupo de amigos e
a quantidade de pessoas do grupo de amigos e  a quantia gasta por eles. De acordo com o enunciado,
a quantia gasta por eles. De acordo com o enunciado,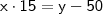
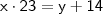


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.