 por luanxd » Dom Fev 07, 2010 20:16
por luanxd » Dom Fev 07, 2010 20:16
Dada a equação
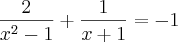
, então:
V=(1)
V=(-1,0,1)
V=(-1,1)
V=(-1,1)
V=(0)
Por favor me ajudem a resolver está equação.
-
luanxd
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 25, 2010 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Fev 08, 2010 15:58
por Molina » Seg Fev 08, 2010 15:58
luanxd escreveu:Dada a equação
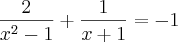
, então:
V=(1)
V=(-1,0,1)
V=(-1,1)
V=(-1,1)
V=(0)
Por favor me ajudem a resolver está equação.
Boa tarde,
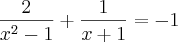
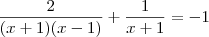
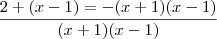

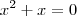
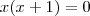
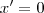
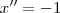

e

seriam as soluções da equação. Porém, temos que

não pode ser solução do sistema, já que substituindo-o os denominadores da fração ficam igual a zero (o que não pode).
Resposta:
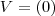
Qualquer dúvida em alguma passagem, informe!
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por luanxd » Seg Fev 08, 2010 18:51
por luanxd » Seg Fev 08, 2010 18:51
Ola Molina obrigado pela ajuda, mas eu não entendi muito bem o finalzinho.
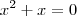
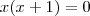
Como você acho o X1 eo X2?
Obrigado pela atenção.
-
luanxd
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 25, 2010 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Fev 08, 2010 18:59
por Molina » Seg Fev 08, 2010 18:59
luanxd escreveu:Ola Molina obrigado pela ajuda, mas eu não entendi muito bem o finalzinho.
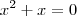
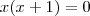
Como você acho o X1 eo X2?
Obrigado pela atenção.
Chegamos até aqui:
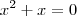
Agora vou fatorar esse termo, colocando x em evidência:
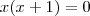
Temos dois "números"

e

que multiplicados dão
zero. Como o produto é 0, ou o primeiro é igual a 0 ou o segundo é igual a 0. E foi isso que eu fiz:

(ou seja, o primeiro termo desse produto é igual a zero)
Note que substituindo 0 por x a equação é válida, pois ficamos com 0*(0+1)=0*1=0E fazemos a mesma coisa com o segundo termo, igualando-o a zero:
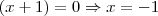

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por luanxd » Ter Fev 09, 2010 11:06
por luanxd » Ter Fev 09, 2010 11:06
Obrigado!
-
luanxd
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Seg Jan 25, 2010 23:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fuvest
por CaAtr » Sex Abr 02, 2010 16:39
- 5 Respostas
- 4657 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 14:27
Sistemas de Equações
-
- LOG FUVEST
por PHANIE » Ter Abr 12, 2011 13:22
- 1 Respostas
- 14745 Exibições
- Última mensagem por Molina

Ter Abr 12, 2011 15:13
Logaritmos
-
- FUVEST 1
 por PHANIE » Ter Abr 26, 2011 15:53
por PHANIE » Ter Abr 26, 2011 15:53
- 3 Respostas
- 14143 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 04, 2011 12:17
Geometria Plana
-
- fuvest 2
por PHANIE » Ter Abr 26, 2011 15:57
- 3 Respostas
- 5030 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 04, 2011 12:33
Geometria Plana
-
- fuvest
por karen » Qua Nov 28, 2012 14:48
- 1 Respostas
- 1299 Exibições
- Última mensagem por young_jedi

Qua Nov 28, 2012 16:10
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
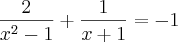 , então:
, então:
, então:
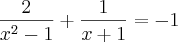
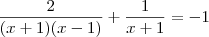
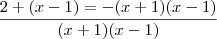

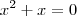
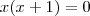
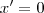
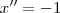
 e
e  seriam as soluções da equação. Porém, temos que
seriam as soluções da equação. Porém, temos que  não pode ser solução do sistema, já que substituindo-o os denominadores da fração ficam igual a zero (o que não pode).
não pode ser solução do sistema, já que substituindo-o os denominadores da fração ficam igual a zero (o que não pode).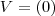


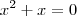
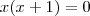

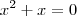
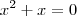
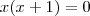
 e
e  que multiplicados dão zero. Como o produto é 0, ou o primeiro é igual a 0 ou o segundo é igual a 0. E foi isso que eu fiz:
que multiplicados dão zero. Como o produto é 0, ou o primeiro é igual a 0 ou o segundo é igual a 0. E foi isso que eu fiz: (ou seja, o primeiro termo desse produto é igual a zero)
(ou seja, o primeiro termo desse produto é igual a zero)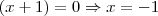



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
