 por Victor985 » Dom Nov 03, 2013 18:16
por Victor985 » Dom Nov 03, 2013 18:16
Considere a equação

onde x, y e z são números reais. É verdade que:
a) a equação admite uma solução
b) em qualquer solução,
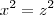
c) em qualquer solução,

d) em qualquer solução,
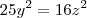
e) em qualquer solução,
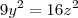
Eu já tentei resolvê-lo várias vezes e não consegui.
-
Victor985
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Nov 02, 2013 12:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Seg Nov 04, 2013 19:22
por e8group » Seg Nov 04, 2013 19:22
Basta obter a solução geral do sistema linear homogêneo e comparar o resultado com as alternativas .
Inicialmente , temos o sistema escrito sob a forma :

. (A,B,C são as mesmas matrizes colunas dadas )
Esta expressão é equivalente a

, onde
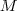
é uma matriz
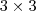
em que suas colunas 1,2,3 são respectivamente as matrizes colunas
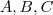
.
Graças ao wolfram alpha , já verificamos que
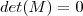
, veja
http://www.wolframalpha.com/input/?i=de ... C3%7D%7D++ .
Isto significa que a matriz
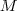
não é invertível o que implica que o sistema é incompatível (não há solução ) ou compatível indeterminado (infinitas soluções ) , mas como todo sistema linear homogêneo possui pelo menos a solução trivial que é o vetor nulo
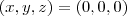
,então por
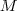
ser singular , concluímos que o sistema em questão é compatível e indeterminado (possui infinitas soluções ) . Aqui já eliminamos o item (a) .
Segundo wolfram alpha ,solução geral do sistema é

e
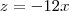
. Mas faça as contas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Victor985 » Ter Nov 05, 2013 18:24
por Victor985 » Ter Nov 05, 2013 18:24
Obrigado pela ajuda.
-
Victor985
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Nov 02, 2013 12:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [P.A.] Exercício
por Cleyson007 » Dom Mai 25, 2008 13:02
- 1 Respostas
- 6563 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 13:20
Progressões
-
- Exercício de PA
por Cleyson007 » Dom Jun 01, 2008 02:45
- 1 Respostas
- 11349 Exibições
- Última mensagem por admin

Dom Jun 01, 2008 14:31
Progressões
-
- Exercício de PA e PG
por Cleyson007 » Sáb Jun 14, 2008 01:21
- 3 Respostas
- 15309 Exibições
- Última mensagem por DanielFerreira

Sex Jul 24, 2009 11:59
Progressões
-
- exercicio de P.G.
por Gir » Qui Jul 02, 2009 18:21
- 3 Respostas
- 4428 Exibições
- Última mensagem por Gir

Sex Jul 03, 2009 10:12
Progressões
-
- exercicio de P.G.
por Gir » Seg Jul 06, 2009 10:54
- 1 Respostas
- 3374 Exibições
- Última mensagem por Marcampucio

Seg Jul 06, 2009 16:33
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

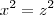

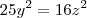
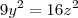


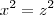

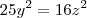
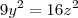

 . (A,B,C são as mesmas matrizes colunas dadas )
. (A,B,C são as mesmas matrizes colunas dadas ) , onde
, onde 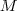 é uma matriz
é uma matriz 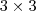 em que suas colunas 1,2,3 são respectivamente as matrizes colunas
em que suas colunas 1,2,3 são respectivamente as matrizes colunas 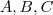 .
. 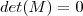 , veja
, veja 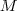 não é invertível o que implica que o sistema é incompatível (não há solução ) ou compatível indeterminado (infinitas soluções ) , mas como todo sistema linear homogêneo possui pelo menos a solução trivial que é o vetor nulo
não é invertível o que implica que o sistema é incompatível (não há solução ) ou compatível indeterminado (infinitas soluções ) , mas como todo sistema linear homogêneo possui pelo menos a solução trivial que é o vetor nulo 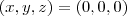 ,então por
,então por 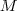 ser singular , concluímos que o sistema em questão é compatível e indeterminado (possui infinitas soluções ) . Aqui já eliminamos o item (a) .
ser singular , concluímos que o sistema em questão é compatível e indeterminado (possui infinitas soluções ) . Aqui já eliminamos o item (a) .  e
e 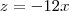 . Mas faça as contas .
. Mas faça as contas .
