equação

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

equação

Regras do fórum
Responder

equação

Mensagempor bob » Qui Nov 12, 2009 10:55

bom dia, é a 1ª vez que acesso o site, faço um cursinho e tenho alguns exercicios a resolver, porem um eu não consegui, é simples mas eu não consigo.
2C+1506.21/4c = 401.41

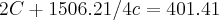
espero que possa me ajudar...até mais
bob
Novo Usuário
Novo Usuário
 
Mensagens: 3
Registrado em: Qui Nov 12, 2009 10:44
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo

Re: equação

Mensagempor Molina » Qui Nov 12, 2009 13:19

Bom dia, Bob!

A questão como você colocou é ambigua, pois nao sabemos se o 4C está dividindo 1506.21 ou dividindo o 2C + 1506.21

Confirme então qual dos casos que é, ok?

:y:
Diego Molina | CV | FB | .COM
Equipe AjudaMatemática.com


"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
Avatar do usuário
Molina
Colaborador Moderador - Professor
Colaborador Moderador - Professor
 
Mensagens: 1551
Registrado em: Dom Jun 01, 2008 14:10
Formação Escolar: GRADUAÇÃO
Área/Curso: Licenciatura em Matemática - UFSC
Andamento: formado
Voltar ao topo

Re: equação

Mensagempor bob » Qui Nov 12, 2009 13:45

me desculpa pela má colocação o correto seria:
2C+(1506,21/4C) = 401,41

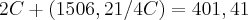
mais uma vez desculpa e obrigado...
bob
Novo Usuário
Novo Usuário
 
Mensagens: 3
Registrado em: Qui Nov 12, 2009 10:44
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo

Re: equação

Mensagempor Molina » Qui Nov 12, 2009 14:08

Sem problemas amigo.

Note que do lado esquerdo temos uma adição de fração.
Por isso precisamo tirar o mmc para começar a resolver:

2C+\frac{1506,21}{4C} = 401,41

\frac{8c^2+1506,21}{4C} = 401,41

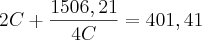
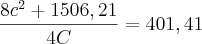
Passamos o 4C para o outro lado fazendo a operação inversa (multiplicando):

8c^2+1506,21 = 401,41*4C

8c^2+1506,21 = 1605,64C

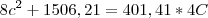
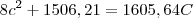
Passando o que está do lado direito para o lado esquerdo:

8c^2-1605,64C+1506,21 = 0

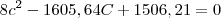
Ou seja, chegamos em uma equação do 2° grau.
Para resolver utilize a Fórmula de Báskara.

Bom estudo, :y:
Diego Molina | CV | FB | .COM
Equipe AjudaMatemática.com


"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
Avatar do usuário
Molina
Colaborador Moderador - Professor
Colaborador Moderador - Professor
 
Mensagens: 1551
Registrado em: Dom Jun 01, 2008 14:10
Formação Escolar: GRADUAÇÃO
Área/Curso: Licenciatura em Matemática - UFSC
Andamento: formado
Voltar ao topo

Re: equação

Mensagempor bob » Qui Nov 12, 2009 14:09

muito, muito obrigado mesmo...vcs estão de parabéns pelo site...
bob
Novo Usuário
Novo Usuário
 
Mensagens: 3
Registrado em: Qui Nov 12, 2009 10:44
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo
Responder

Voltar para Sistemas de Equações

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

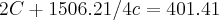
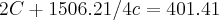
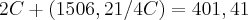
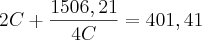
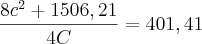
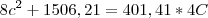
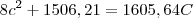
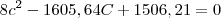
Índice do fórum