 por oliveiracosmo » Sáb Set 01, 2012 19:03
por oliveiracosmo » Sáb Set 01, 2012 19:03
Temos apenas
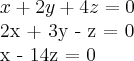
Eu já gastei duas folhas frente e verso tentando resolver, mas não estou conseguindo achar as respostas de cada uma das incógnitas, será simplesmente dizer que o sistema é possível e indeterminada?
-
oliveiracosmo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Set 01, 2012 18:55
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Set 01, 2012 22:10
por DanielFerreira » Sáb Set 01, 2012 22:10
Olá
Oliveiracosmo,
seja bem-vindo!
Da última equação:
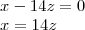
Substituindo o 'valor' de x nas outras equações teremos:
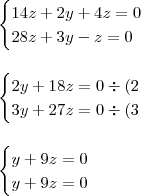
Resolvendo o sistema por substituição...
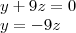
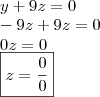
Podemos concluir que o sistema é
indeterminado.
Espero ter ajudado!
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por oliveiracosmo » Dom Set 02, 2012 14:25
por oliveiracosmo » Dom Set 02, 2012 14:25
Obrigado, ajudou bastante, sempre que poder estarei aqui no fórum.
-
oliveiracosmo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Set 01, 2012 18:55
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Seg Set 03, 2012 19:31
por DanielFerreira » Seg Set 03, 2012 19:31
Não há de quê e volte sempre!!
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resolução de Um sistema Linear
por fttofolo » Qua Set 21, 2011 19:30
- 2 Respostas
- 4569 Exibições
- Última mensagem por fttofolo

Qua Set 21, 2011 21:47
Sistemas de Equações
-
- [Sistema Não-Linear de Equação] Resolução
por mdiego » Qui Jul 05, 2012 00:14
- 0 Respostas
- 4248 Exibições
- Última mensagem por mdiego

Qui Jul 05, 2012 00:14
Sistemas de Equações
-
- SISTEMA LINEAR DÚVIDA
por Fernanda Lauton » Qui Jun 10, 2010 19:43
- 4 Respostas
- 3353 Exibições
- Última mensagem por MarceloFantini

Sáb Jun 12, 2010 12:37
Sistemas de Equações
-
- Sistema Linear - Dúvida
por Veronica » Seg Abr 23, 2012 22:34
- 0 Respostas
- 1158 Exibições
- Última mensagem por Veronica

Seg Abr 23, 2012 22:34
Sistemas de Equações
-
- [Sistema linear dúvida]
por Aprendiz2012 » Dom Ago 26, 2012 21:26
- 1 Respostas
- 1621 Exibições
- Última mensagem por MarceloFantini

Dom Ago 26, 2012 22:57
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
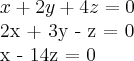

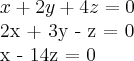

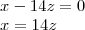
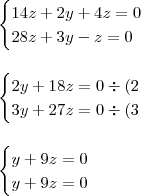
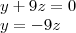
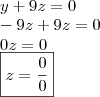




 .
.
 :
: