 por silvia fillet » Qua Jun 13, 2012 11:23
por silvia fillet » Qua Jun 13, 2012 11:23
Considere que três pessoas, Pedro, Carlos e João tem a seguinte relação entre seus salários:
i – Duas vezes o salário de Carlos, menos o salário de João, menos o salário de Pedro é igual a R$ 3000,00.
ii – A soma do salário das três pessoas é igual a R$ 6000,00.
iii – O salário de Pedro, mais duas vezes o salário de João, mais duas vezes o salário de Carlos é igual a R$ 11000,00.
a) Escreva o sistema de equações que representa a relação entre os salários de Pedro, Carlos e João.
b) Escreva a matriz ampliada (ou aumentada) do sistema de equações obtido no item anterior
c) Através do escalonamento da matriz ampliada, reescreva o sistema de equações na forma matricial de maneira que a matriz dos coeficientes esteja na forma triangular superior.
d) Com o resultado do item anterior, obtenha os salários de Pedro, Carlos e João
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por silvia fillet » Qua Jun 13, 2012 11:27
por silvia fillet » Qua Jun 13, 2012 11:27
Bom, comecei assim:
Pedro = x
Carlos = y
João = z
Sistema linear:
-x +2y -z = 3000
x +y +z =6000
x +2y +2z = 11000
matriz aumentada
-1 2 -1 3000
1 1 1 6000
1 2 2 11000
Seria isso para iniciar?
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por Cleyson007 » Qua Jun 13, 2012 12:22
por Cleyson007 » Qua Jun 13, 2012 12:22
Bom dia Silvia!
Isso mesmo

Agora tente resolver o restante.
Quanto ao exercício d, utilize o sistema obtido na letra a para resolvê-lo ok?
Comente qualquer dúvida.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por silvia fillet » Qua Jun 13, 2012 13:19
por silvia fillet » Qua Jun 13, 2012 13:19
Será que posso multiplicar por -1 a primeira equaçao, ficando assim:
1 -2 1 -3000
1 1 1 6000
1 2 2 11000
porque daí enrosquei?
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por silvia fillet » Qua Jun 13, 2012 13:32
por silvia fillet » Qua Jun 13, 2012 13:32
bom resolvi assim:
1 -2 1 -3000
1 1 1 6000
1 2 2 11000
dai fiz L2-L1 e L3 -L1
1 -2 1 -3000
0 3 0 9000
0 4 1 14000
dai o sistema
x -2y +z = -3000
0x +3y +0z = 9000
0x +4y +z = 14000
daí encontrei
y = 3000
z = 2000
x = 1000
seria isso?
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por Cleyson007 » Qua Jun 13, 2012 20:29
por Cleyson007 » Qua Jun 13, 2012 20:29
Boa noite Sílvia!
Sílvia, são muitas as formas para se resolver exercícios desse tipo..
Sua resposta está correta

Bom, eu utilizaria o método da adição começando pelas duas primeira equações, pois eliminaria o "x" e o '"z" encontrando o valor de y.
Espero ter ajudado.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por silvia fillet » Qua Jun 13, 2012 22:19
por silvia fillet » Qua Jun 13, 2012 22:19
Eu também acho mais fácil calcular pela adição e subtracção, só que o exercício pede escalonamento matricial
-
silvia fillet
- Usuário Parceiro

-
- Mensagens: 89
- Registrado em: Qua Out 12, 2011 21:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por DanielFerreira » Qui Jun 14, 2012 20:13
por DanielFerreira » Qui Jun 14, 2012 20:13
silvia fillet escreveu:Considere que três pessoas, Pedro, Carlos e João tem a seguinte relação entre seus salários:
i – Duas vezes o salário de Carlos, menos o salário de João, menos o salário de Pedro é igual a R$ 3000,00.
ii – A soma do salário das três pessoas é igual a R$ 6000,00.
iii – O salário de Pedro, mais duas vezes o salário de João, mais duas vezes o salário de Carlos é igual a R$ 11000,00.
a) Escreva o sistema de equações que representa a relação entre os salários de Pedro, Carlos e João.
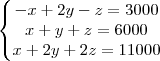
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Qui Jun 14, 2012 20:15
por DanielFerreira » Qui Jun 14, 2012 20:15
silvia fillet escreveu:Considere que três pessoas, Pedro, Carlos e João tem a seguinte relação entre seus salários:
i – Duas vezes o salário de Carlos, menos o salário de João, menos o salário de Pedro é igual a R$ 3000,00.
ii – A soma do salário das três pessoas é igual a R$ 6000,00.
iii – O salário de Pedro, mais duas vezes o salário de João, mais duas vezes o salário de Carlos é igual a R$ 11000,00.
b) Escreva a matriz ampliada (ou aumentada) do sistema de equações obtido no item anterior

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Qui Jun 14, 2012 20:22
por DanielFerreira » Qui Jun 14, 2012 20:22
silvia fillet escreveu:c) Através do escalonamento da matriz ampliada, reescreva o sistema de equações na forma matricial de maneira que a matriz dos coeficientes esteja na forma triangular superior.

==> Fazendo

, fica:

==> Fazendo

, fica:
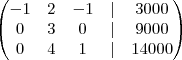
==> Fazendo

, fica:
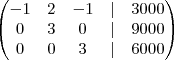
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Qui Jun 14, 2012 20:24
por DanielFerreira » Qui Jun 14, 2012 20:24
silvia fillet escreveu:d) Com o resultado do item anterior, obtenha os salários de Pedro, Carlos e João
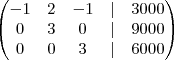
3z = 6000
z = R$ 2.000,003y = 9000
y = R$ 3.000,00- x + 2y - z = 3000
x = 2y - z - 3000
x = 6000 - 2000 - 3000
x = R$ 1.000,00"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistemas Lineares
por Cleyson007 » Sáb Mai 03, 2008 01:50
- 3 Respostas
- 7049 Exibições
- Última mensagem por admin

Dom Mai 04, 2008 13:51
Sistemas de Equações
-
- Sistemas Lineares
por gustavowelp » Sáb Jun 26, 2010 17:05
- 3 Respostas
- 7808 Exibições
- Última mensagem por Douglasm

Dom Jun 27, 2010 09:09
Sistemas de Equações
-
- Sistemas lineares
por Catriane Moreira » Seg Set 06, 2010 18:32
- 1 Respostas
- 2496 Exibições
- Última mensagem por Molina

Seg Set 06, 2010 19:13
Sistemas de Equações
-
- sistemas lineares
por angeloka » Sáb Nov 27, 2010 17:59
- 1 Respostas
- 2638 Exibições
- Última mensagem por Neperiano

Sáb Nov 27, 2010 19:02
Sistemas de Equações
-
- sistemas lineares
 por angeloka » Sáb Nov 27, 2010 22:10
por angeloka » Sáb Nov 27, 2010 22:10
- 0 Respostas
- 1823 Exibições
- Última mensagem por angeloka

Sáb Nov 27, 2010 22:10
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





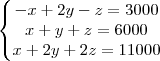


 , fica:
, fica:
 , fica:
, fica: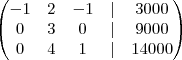
 , fica:
, fica: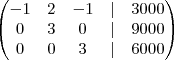

 .
.



