 por nicolegcg » Ter Jun 12, 2012 16:24
por nicolegcg » Ter Jun 12, 2012 16:24
Estou com dificuldades neste problema:
Seja a um número racional não nulo. Se b e raíz de 2 são raízes irracionais da equação x³ + ax² - 2x - 2a = 0. Determine o valor de b^4
Comecei fazendo ruffini por raíz de 2, porém ficou com resto -6a -4raíz2. A partir daí não sei continuar :/
-
nicolegcg
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Jun 11, 2012 17:44
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Informática
- Andamento: cursando
 por e8group » Ter Jun 12, 2012 18:36
por e8group » Ter Jun 12, 2012 18:36
Boa tarde nicolegcg ,
Tente dividir a equação por
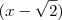
. Daí você pode achar o valor de "a " igualando o resto da divisão a zero e em consequência obtera o valor de "b" .
Desta forma ,
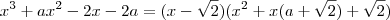
.
tente aí agora ,abraços !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Resto
por thadeu » Dom Nov 22, 2009 23:03
- 2 Respostas
- 1581 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 05:58
Álgebra Elementar
-
- Resto Divisão
por Cleyson007 » Dom Jul 05, 2009 19:55
- 1 Respostas
- 2114 Exibições
- Última mensagem por Cleyson007

Qua Jul 08, 2009 21:08
Polinômios
-
- Resto da divisão
por ronie_mota » Dom Jul 26, 2009 16:25
- 0 Respostas
- 2549 Exibições
- Última mensagem por ronie_mota

Dom Jul 26, 2009 16:25
Álgebra Elementar
-
- Resto da divisão
por thadeu » Qua Nov 18, 2009 19:22
- 2 Respostas
- 2450 Exibições
- Última mensagem por thadeu

Dom Nov 22, 2009 17:02
Álgebra Elementar
-
- Resto de uma divisão
por baianinha » Seg Ago 29, 2011 12:20
- 1 Respostas
- 1919 Exibições
- Última mensagem por LuizAquino

Seg Ago 29, 2011 13:51
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


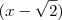 . Daí você pode achar o valor de "a " igualando o resto da divisão a zero e em consequência obtera o valor de "b" .
. Daí você pode achar o valor de "a " igualando o resto da divisão a zero e em consequência obtera o valor de "b" .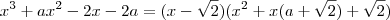 .
.

 .
.



