 por nathyn » Seg Jan 30, 2012 15:18
por nathyn » Seg Jan 30, 2012 15:18
oii, to meia enrolada na resolução dessas equações, nao sei se estou fazendo certo ou se tem alguma maneira mais simples de resolver, se alguem puder ajudar, por favor...
1ª)
![\frac{1}{\sqrt[]{x+\sqrt[]{{x}^{2}-1}}} + \frac{1}{\sqrt[]{x-\sqrt[]{{x}^{2}-1}}} = \sqrt[]{2({x}^{2}+1)} \frac{1}{\sqrt[]{x+\sqrt[]{{x}^{2}-1}}} + \frac{1}{\sqrt[]{x-\sqrt[]{{x}^{2}-1}}} = \sqrt[]{2({x}^{2}+1)}](/latexrender/pictures/6fd065882dbf99bef96077fb0216694a.png)
Eu fiz o mmc e encontrei:
![\frac{\sqrt[]{x-\sqrt[]{{x}^{2}-1}} + \sqrt[]{x+\sqrt[]{{x}^{2}-1}}}{x-\sqrt[]{{x}^{2}-1}} = \frac{x - \sqrt[]{{2x}^{4}-2}}{x-\sqrt[]{{x}^{2}-1}} \frac{\sqrt[]{x-\sqrt[]{{x}^{2}-1}} + \sqrt[]{x+\sqrt[]{{x}^{2}-1}}}{x-\sqrt[]{{x}^{2}-1}} = \frac{x - \sqrt[]{{2x}^{4}-2}}{x-\sqrt[]{{x}^{2}-1}}](/latexrender/pictures/74bc0a3ce986f65d8517abc9a314c907.png)
Elevei ambos os lados ao quadrado e ficou...
![{x-\sqrt[]{{x}^{2}-1} + 2x-2 \sqrt[]{{x}^{2}-1} + {x+\sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} \rightarrow {x-\sqrt[]{{x}^{2}-1} + 2x-2 \sqrt[]{{x}^{2}-1} + {x+\sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} \rightarrow](/latexrender/pictures/02c500a3ce9bb7236d5fd90f0c05d34c.png)
![{2x + 2x-2 \sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} {2x + 2x-2 \sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2}](/latexrender/pictures/2d5ac3e828002fa973385eeb96ce23fd.png)
Daí então não sei mais como fazer... =/
2ª)
![\frac{x + \sqrt[]{3}}{\sqrt[]{x} + \sqrt[]{x+\sqrt[]{3}}} + \frac{x - \sqrt[]{3}}{\sqrt[]{x} - \sqrt[]{x-\sqrt[]{3}}}= \sqrt[]{x} \frac{x + \sqrt[]{3}}{\sqrt[]{x} + \sqrt[]{x+\sqrt[]{3}}} + \frac{x - \sqrt[]{3}}{\sqrt[]{x} - \sqrt[]{x-\sqrt[]{3}}}= \sqrt[]{x}](/latexrender/pictures/75f9d058b62079d440a8acee3695984c.png)
Tirando o mmc encontrei:
![\frac{-x\sqrt[]{x-\sqrt[]{3}} -\sqrt[]{3x - \sqrt[]{3}} + x\sqrt[]{x} + x\sqrt[]{x + \sqrt[]{3}} - \sqrt[]{3x + \sqrt[]{3}} = -\sqrt[]{{x}^{3} - 3x}}{x - \sqrt[]{{x}^{2} - 3}} \frac{-x\sqrt[]{x-\sqrt[]{3}} -\sqrt[]{3x - \sqrt[]{3}} + x\sqrt[]{x} + x\sqrt[]{x + \sqrt[]{3}} - \sqrt[]{3x + \sqrt[]{3}} = -\sqrt[]{{x}^{3} - 3x}}{x - \sqrt[]{{x}^{2} - 3}}](/latexrender/pictures/4e69b1fee8c11edf86498149c8751ad5.png)
nem sei se está certo, mas...
Me ajudem ae por favor...
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por nathyn » Seg Jan 30, 2012 19:15
por nathyn » Seg Jan 30, 2012 19:15
Aaah brigadão, a primeira eu entendi e consegui encontrar a resposta muito obrigada mesmo. Já a segunda eu não entendi o que foi feito, vc multiplicou em cima e em baica em cada fraçao pela mesma coisa? Pq foi feito isso e quando eu posso usar esse tipo de simplificação?
Desculpa, é que não tenho uma boa base...
d qualquer forma, muito obrigada.
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Seg Jan 30, 2012 23:48
por LuizAquino » Seg Jan 30, 2012 23:48
nathyn escreveu:Já a segunda eu não entendi o que foi feito, vc multiplicou em cima e em baica em cada fraçao pela mesma coisa?
Sim, eu multipliquei o numerador e o denominador por uma mesma expressão.
nathyn escreveu:Pq foi feito isso e quando eu posso usar esse tipo de simplificação?
Isso foi feito para simplificar a raiz que havia no denominador.
A ideia é parecida com a que usamos quando queremos racionalizar denominadores.
nathyn escreveu:Desculpa, é que não tenho uma boa base...
Eu recomendo que você assista as vídeo-aulas do Nerckie. Elas estão disponíveis no canal dele no YouTube:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por nathyn » Ter Jan 31, 2012 10:42
por nathyn » Ter Jan 31, 2012 10:42
aah ta, entendi... pq se multiplicar em cima e em baixo pela mesma coisa não altera a fração...
Brigadão e vou dah uma assistida sim.
Muito obrigada. Fica com Deus ;D
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7735 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13238 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13030 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6098 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8720 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{1}{\sqrt[]{x+\sqrt[]{{x}^{2}-1}}} + \frac{1}{\sqrt[]{x-\sqrt[]{{x}^{2}-1}}} = \sqrt[]{2({x}^{2}+1)} \frac{1}{\sqrt[]{x+\sqrt[]{{x}^{2}-1}}} + \frac{1}{\sqrt[]{x-\sqrt[]{{x}^{2}-1}}} = \sqrt[]{2({x}^{2}+1)}](/latexrender/pictures/6fd065882dbf99bef96077fb0216694a.png)
![\frac{\sqrt[]{x-\sqrt[]{{x}^{2}-1}} + \sqrt[]{x+\sqrt[]{{x}^{2}-1}}}{x-\sqrt[]{{x}^{2}-1}} = \frac{x - \sqrt[]{{2x}^{4}-2}}{x-\sqrt[]{{x}^{2}-1}} \frac{\sqrt[]{x-\sqrt[]{{x}^{2}-1}} + \sqrt[]{x+\sqrt[]{{x}^{2}-1}}}{x-\sqrt[]{{x}^{2}-1}} = \frac{x - \sqrt[]{{2x}^{4}-2}}{x-\sqrt[]{{x}^{2}-1}}](/latexrender/pictures/74bc0a3ce986f65d8517abc9a314c907.png)
![{x-\sqrt[]{{x}^{2}-1} + 2x-2 \sqrt[]{{x}^{2}-1} + {x+\sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} \rightarrow {x-\sqrt[]{{x}^{2}-1} + 2x-2 \sqrt[]{{x}^{2}-1} + {x+\sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} \rightarrow](/latexrender/pictures/02c500a3ce9bb7236d5fd90f0c05d34c.png)
![{2x + 2x-2 \sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} {2x + 2x-2 \sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2}](/latexrender/pictures/2d5ac3e828002fa973385eeb96ce23fd.png)
![\frac{x + \sqrt[]{3}}{\sqrt[]{x} + \sqrt[]{x+\sqrt[]{3}}} + \frac{x - \sqrt[]{3}}{\sqrt[]{x} - \sqrt[]{x-\sqrt[]{3}}}= \sqrt[]{x} \frac{x + \sqrt[]{3}}{\sqrt[]{x} + \sqrt[]{x+\sqrt[]{3}}} + \frac{x - \sqrt[]{3}}{\sqrt[]{x} - \sqrt[]{x-\sqrt[]{3}}}= \sqrt[]{x}](/latexrender/pictures/75f9d058b62079d440a8acee3695984c.png)
![\frac{-x\sqrt[]{x-\sqrt[]{3}} -\sqrt[]{3x - \sqrt[]{3}} + x\sqrt[]{x} + x\sqrt[]{x + \sqrt[]{3}} - \sqrt[]{3x + \sqrt[]{3}} = -\sqrt[]{{x}^{3} - 3x}}{x - \sqrt[]{{x}^{2} - 3}} \frac{-x\sqrt[]{x-\sqrt[]{3}} -\sqrt[]{3x - \sqrt[]{3}} + x\sqrt[]{x} + x\sqrt[]{x + \sqrt[]{3}} - \sqrt[]{3x + \sqrt[]{3}} = -\sqrt[]{{x}^{3} - 3x}}{x - \sqrt[]{{x}^{2} - 3}}](/latexrender/pictures/4e69b1fee8c11edf86498149c8751ad5.png)

![\frac{1}{\sqrt[]{x+\sqrt[]{{x}^{2}-1}}} + \frac{1}{\sqrt[]{x-\sqrt[]{{x}^{2}-1}}} = \sqrt[]{2({x}^{2}+1)} \frac{1}{\sqrt[]{x+\sqrt[]{{x}^{2}-1}}} + \frac{1}{\sqrt[]{x-\sqrt[]{{x}^{2}-1}}} = \sqrt[]{2({x}^{2}+1)}](/latexrender/pictures/6fd065882dbf99bef96077fb0216694a.png)
![\frac{\sqrt[]{x-\sqrt[]{{x}^{2}-1}} + \sqrt[]{x+\sqrt[]{{x}^{2}-1}}}{x-\sqrt[]{{x}^{2}-1}} = \frac{x - \sqrt[]{{2x}^{4}-2}}{x-\sqrt[]{{x}^{2}-1}} \frac{\sqrt[]{x-\sqrt[]{{x}^{2}-1}} + \sqrt[]{x+\sqrt[]{{x}^{2}-1}}}{x-\sqrt[]{{x}^{2}-1}} = \frac{x - \sqrt[]{{2x}^{4}-2}}{x-\sqrt[]{{x}^{2}-1}}](/latexrender/pictures/74bc0a3ce986f65d8517abc9a314c907.png)
![{x-\sqrt[]{{x}^{2}-1} + 2x-2 \sqrt[]{{x}^{2}-1} + {x+\sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} \rightarrow {x-\sqrt[]{{x}^{2}-1} + 2x-2 \sqrt[]{{x}^{2}-1} + {x+\sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} \rightarrow](/latexrender/pictures/02c500a3ce9bb7236d5fd90f0c05d34c.png)
![{2x + 2x-2 \sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2} {2x + 2x-2 \sqrt[]{{x}^{2}-1} = {x}^{2}+{2x}^{4}-2-2x\sqrt[]{{2x}^{4}-2}](/latexrender/pictures/2d5ac3e828002fa973385eeb96ce23fd.png)
![\frac{x + \sqrt[]{3}}{\sqrt[]{x} + \sqrt[]{x+\sqrt[]{3}}} + \frac{x - \sqrt[]{3}}{\sqrt[]{x} - \sqrt[]{x-\sqrt[]{3}}}= \sqrt[]{x} \frac{x + \sqrt[]{3}}{\sqrt[]{x} + \sqrt[]{x+\sqrt[]{3}}} + \frac{x - \sqrt[]{3}}{\sqrt[]{x} - \sqrt[]{x-\sqrt[]{3}}}= \sqrt[]{x}](/latexrender/pictures/75f9d058b62079d440a8acee3695984c.png)
![\frac{-x\sqrt[]{x-\sqrt[]{3}} -\sqrt[]{3x - \sqrt[]{3}} + x\sqrt[]{x} + x\sqrt[]{x + \sqrt[]{3}} - \sqrt[]{3x + \sqrt[]{3}} = -\sqrt[]{{x}^{3} - 3x}}{x - \sqrt[]{{x}^{2} - 3}} \frac{-x\sqrt[]{x-\sqrt[]{3}} -\sqrt[]{3x - \sqrt[]{3}} + x\sqrt[]{x} + x\sqrt[]{x + \sqrt[]{3}} - \sqrt[]{3x + \sqrt[]{3}} = -\sqrt[]{{x}^{3} - 3x}}{x - \sqrt[]{{x}^{2} - 3}}](/latexrender/pictures/4e69b1fee8c11edf86498149c8751ad5.png)

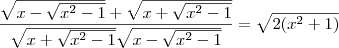
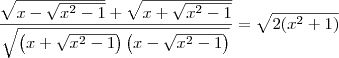
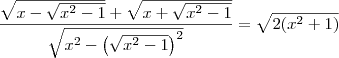
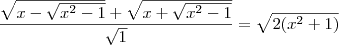
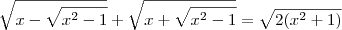
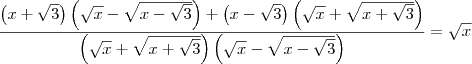
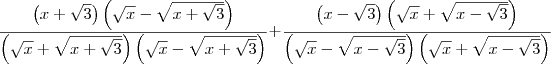
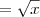
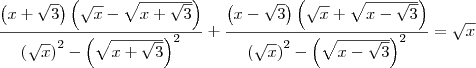
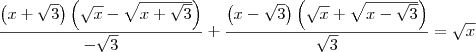




![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.