 por ursoforte » Seg Ago 15, 2011 13:06
por ursoforte » Seg Ago 15, 2011 13:06
Eu sei ate resolver equação do 2º grau usando o delta e Baskara, mas tenho um indice muito grande em resolver problemas como esse "A área de um retângulo é de 64cm quadrado . Nessas condições, determine as dimensões do retângulo sabendo que o comprimento mede (x+6) m e a largura mede (x- 6) m.". A minha dificuldade esta em montar a equação para resolver.
Se alguem souber a onde posso encontrar alguns problemas que ensine fazer as formulas, me indique pra que posso praticar;
Desde ja estou agradecido.
-
ursoforte
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Ago 15, 2011 09:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Molina » Seg Ago 15, 2011 13:34
por Molina » Seg Ago 15, 2011 13:34
Bom dia!
ursoforte escreveu:Eu sei ate resolver equação do 2º grau usando o delta e Baskara, mas tenho um indice muito grande em resolver problemas como esse "A área de um retângulo é de 64cm quadrado . Nessas condições, determine as dimensões do retângulo sabendo que o comprimento mede (x+6) m e a largura mede (x- 6) m.". A minha dificuldade esta em montar a equação para resolver.
Primeiro de tudo faça um desenho de um retângulo e nomeie os lados, conforme consta no enunciado. Os lados maiores terão
x+6 metros e os lados menores terão
x-6 metros.
A área do retângulo é dado por:

, onde
b é a base do retângulo e
h é a altura do retângulo. Perceba que dessa equação você já tem todas as informações (A, b e h):


Agora você precisa descobrir o valor de x para que isso ocorra. Para isso, faça a distributiva e vai chegar em uma equação de 2º grau.
Faça e poste suas tentativas. Caso tenha dúvida, avise!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por ursoforte » Seg Ago 15, 2011 19:12
por ursoforte » Seg Ago 15, 2011 19:12
Infelismente não consegui desenvolver a equação mas vou postar aqui até a onde consegui
x{2}+6x-36
Delta=6{2}-4*1*(-36)
Delta=36-4*(-36)
Delta=-4
não dava nem mais pra continuar pois o resultado na minha apostila e 16cm e 4cm
-
ursoforte
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Ago 15, 2011 09:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Molina » Seg Ago 15, 2011 21:42
por Molina » Seg Ago 15, 2011 21:42
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por ursoforte » Qua Ago 17, 2011 19:40
por ursoforte » Qua Ago 17, 2011 19:40
Obrigado,
estou reforçando meus conhecimentos em matemática básica, e logo estarei postando minhas dúvidas, pois estudo através de livros e pesquinas na internet, tenho dificuldade financeira para pagar um professor particular,e pela graça de Deus encontrei alguém solidários e com boa disposição como você pra ajudar a todos neste forum.
fique na graça de Deus
Raimundo
-
ursoforte
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Ago 15, 2011 09:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Molina » Qua Ago 17, 2011 20:02
por Molina » Qua Ago 17, 2011 20:02
Boa noite, Raimundo!
ursoforte escreveu:Obrigado,
estou reforçando meus conhecimentos em matemática básica, e logo estarei postando minhas dúvidas, pois estudo através de livros e pesquinas na internet, tenho dificuldade financeira para pagar um professor particular,e pela graça de Deus encontrei alguém solidários e com boa disposição como você pra ajudar a todos neste forum.
fique na graça de Deus
Raimundo
Garanto que o fórum é tão produtivo quanto a contratação de um professor particular. Se você fizer bom uso deste espaço seus objetivos serão alcançados em relação a matemática. Mas para isso, muito empenho e dedicação.
Conte conosco!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problemas equação 1° grau, dúvida.
por Clairelz12 » Sáb Ago 29, 2009 03:44
- 4 Respostas
- 7462 Exibições
- Última mensagem por Elcioschin

Sáb Ago 29, 2009 19:18
Álgebra Elementar
-
- Problemas de equação e sistemas de 1º grau
por gigante2010 » Dom Out 17, 2010 15:22
- 3 Respostas
- 4225 Exibições
- Última mensagem por MarceloFantini

Dom Out 17, 2010 23:00
Tópicos sem Interação (leia as regras)
-
- Problemas de equação do primeiro grau.
por Andrewo » Seg Fev 20, 2012 08:55
- 2 Respostas
- 5681 Exibições
- Última mensagem por Andrewo

Seg Fev 20, 2012 11:35
Sistemas de Equações
-
- Problemas de equação do primeiro grau.
por Andrewo » Qui Fev 23, 2012 18:00
- 3 Respostas
- 4539 Exibições
- Última mensagem por LuizAquino

Sex Fev 24, 2012 10:56
Sistemas de Equações
-
- Problemas de equação do primeiro grau III
por Andrewo » Seg Fev 27, 2012 11:58
- 3 Respostas
- 4159 Exibições
- Última mensagem por MarceloFantini

Ter Fev 28, 2012 16:04
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , onde
, onde 



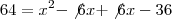





 .
.



