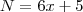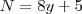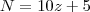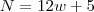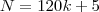por Raphael Feitas10 » Seg Jul 04, 2011 23:33
por Raphael Feitas10 » Seg Jul 04, 2011 23:33
Deisy possui eu um certo numeros de mudas que é inferior a 700.Quando conta de 6 em 6,de 8 em 8,de 10 em 10 ou de 12 em 12,verifica que sobram 5,mas quando conta de 11 em 11,não sobram nenhuma.Calcule o numero de mudas.R: 605
Brother eu tirei o mmc de 6 8 10 e 12 mas mas ñ obtive o resultado me ajuda aew parceiro...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Molina » Ter Jul 05, 2011 13:14
por Molina » Ter Jul 05, 2011 13:14
Bom dia.
Lendo o enunciado de um modo mais fácil você precisa achar um número
N menor do que 700 que seja múltiplo de 11 (já que sua divisão é exata). Além disso, precisa encontrar
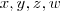
tal que:
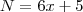
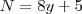
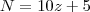
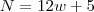
Ou seja, N pode ser escrito da seguinte forma:
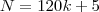
De valores para
k e verifique se
N será múltiplo de 11.
Qualquer dúvida, informe!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


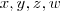 tal que:
tal que: