 por Raphael Feitas10 » Sex Jun 10, 2011 22:33
por Raphael Feitas10 » Sex Jun 10, 2011 22:33
Numa caixa existe bolas brancas e bolas pretas. Se tirarmos 16 bolas brancas, a razão entre as bolas brancas e as pretas será de 1 para 3. Em seguida, retiram-se 7 bolas pretas, restando na caixa a razão entre 1 bola branca para 2 bolas pretas. Determine quantas bolas de cada cor havia inicialmente na caixa.R: 23 brancas e 21 pretas.
Brother me ajuda mais umas vez conseguei fazer ate aqui mas ñ achei a resposta,me ajuda aew desde já agradecido...
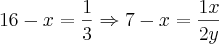
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por deangelo » Sáb Jun 11, 2011 02:04
por deangelo » Sáb Jun 11, 2011 02:04
Equacionando o problema, temos
b = número de bolas brancas
p = números de bolas pretas
Assim obtemos o sistema:
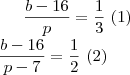
Resolvendo:
Isolando p em (1), temos
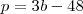
Agora substituindo p em (2), temos
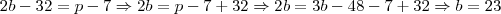
Agora que temos b, calculamos o valor de p

Portanto a quantidade inicial de bolas brancas é de 23, e de pretas 21.
"É por intuição que descobrimos, e pela lógica que provamos". [Henri Poincaré]
-

deangelo
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Out 11, 2010 03:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática-UFES
- Andamento: cursando
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- RAZÃO
por hevhoram » Qua Jun 02, 2010 11:50
- 1 Respostas
- 1544 Exibições
- Última mensagem por Molina

Qua Jun 02, 2010 18:43
Álgebra Elementar
-
- razao
por hevhoram » Qua Jun 02, 2010 20:14
- 2 Respostas
- 1686 Exibições
- Última mensagem por hevhoram

Qui Jun 03, 2010 20:42
Álgebra Elementar
-
- Razão
por Guaciara » Qui Set 23, 2010 22:40
- 2 Respostas
- 2416 Exibições
- Última mensagem por Guaciara

Qui Set 23, 2010 23:31
Conversão de Unidades
-
- razão
por angeloka » Sex Out 15, 2010 19:29
- 8 Respostas
- 6817 Exibições
- Última mensagem por MarceloFantini

Sáb Out 23, 2010 01:41
Álgebra Elementar
-
- PA com razão 0,3
por gustavowelp » Sex Nov 19, 2010 08:42
- 5 Respostas
- 3463 Exibições
- Última mensagem por 0 kelvin

Sex Nov 19, 2010 15:51
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
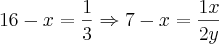


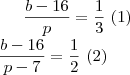
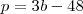
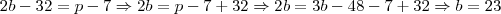


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.