 por stuart clark » Seg Mai 30, 2011 00:31
por stuart clark » Seg Mai 30, 2011 00:31
If
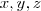
are real no. such that
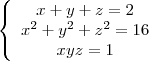
.Then Calculate value of
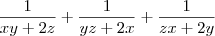
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por FilipeCaceres » Seg Mai 30, 2011 01:34
por FilipeCaceres » Seg Mai 30, 2011 01:34
Note that

,
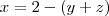
, and
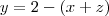
.
From here, notice that
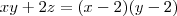
,
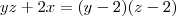
, and

.
It should be clear that what we need to do is construct a polynomial with

as roots.
Firstly, construct a polynomial with x, y, z as roots. From

and

, get the equation

.
Thus a cubic with roots x, y, z is
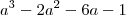
.
A cubic with roots

is
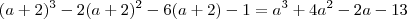
.
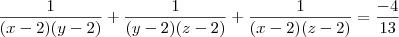
Answer:
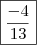
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por stuart clark » Seg Mai 30, 2011 06:27
por stuart clark » Seg Mai 30, 2011 06:27
Thanks FilipeCaceres
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
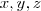 are real no. such that
are real no. such that 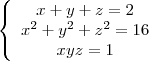 .Then Calculate value of
.Then Calculate value of 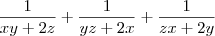

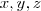 are real no. such that
are real no. such that  .Then Calculate value of
.Then Calculate value of 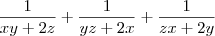

 ,
, 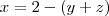 , and
, and 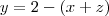 .
.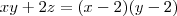 ,
, 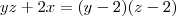 , and
, and  .
. as roots.
as roots. and
and  , get the equation
, get the equation  .
.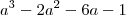 .
. is
is 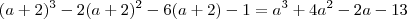 .
.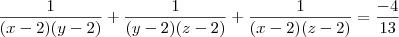
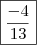


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.