 por lucas7 » Qua Fev 23, 2011 20:15
por lucas7 » Qua Fev 23, 2011 20:15
Dois números estão na razão

. Acrescentando-se 2 a cada um, as somas ficarão na razão 3 para 5. Calcule o produto dos números.
Minha ultima tentativa:
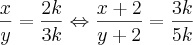
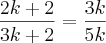

?!?!?!
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por Elcioschin » Qua Fev 23, 2011 20:38
por Elcioschin » Qua Fev 23, 2011 20:38
x/y = 2/3 -----> y = 3x/2
(x + 2)/(y + 2) = 3/5 ----> 5*(x + 2) = 3*(y + 2) ----> 5x + 10 = 3y + 6 ----> 5x + 4 = 3y
5x + 4 = 3*(3x/2) ----> 5x + 4 = 9x/2 ----> 10x + 8 = 9x ----> x = - 8
y = 3x/2 -----> y = 3*(-8)/2 ----> y = - 12
x*y = (-8)*(-12) ----> x*y = 96
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por lucas7 » Qua Fev 23, 2011 21:33
por lucas7 » Qua Fev 23, 2011 21:33
É essa mesmo a resposta. Consegui entender analisando sua resolução. Obrigado.
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por DanielFerreira » Qui Fev 24, 2011 09:30
por DanielFerreira » Qui Fev 24, 2011 09:30
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Elcioschin » Qui Fev 24, 2011 11:04
por Elcioschin » Qui Fev 24, 2011 11:04
Lucas/Danjr5
O valor de k NÃO foi solicitado no enunciado. O que foi pedido foram os valores de x, y
Então, é perda de tempo introduzir uma incógnita auxiliar k
Vejam que, na 1ª condição de Danjr5:
x/y = 2k/3k ----> O k do numerador e do numerador se ANULAM, restando x/y = 2/3
A partir daí vale a minha solução para calcular x, y
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por DanielFerreira » Qui Fev 24, 2011 14:52
por DanielFerreira » Qui Fev 24, 2011 14:52
Elcio,
apenas postei um outro método de resolução; e, minha solução também está correta!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Razão e Proporção
por Danilo Dias Vilela » Qua Mar 03, 2010 00:49
- 1 Respostas
- 2181 Exibições
- Última mensagem por Elcioschin

Qua Mar 03, 2010 13:56
Sistemas de Equações
-
- Razão e proporção
por Catriane Moreira » Seg Set 06, 2010 22:25
- 1 Respostas
- 1962 Exibições
- Última mensagem por DanielRJ

Seg Set 06, 2010 23:42
Matemática Financeira
-
- Razão e proporção x/y=2/3, x+y=10
por lucas7 » Qua Fev 23, 2011 15:44
- 3 Respostas
- 3599 Exibições
- Última mensagem por DanielFerreira

Qua Mar 02, 2011 19:21
Sistemas de Equações
-
- Razão e Proporção
por ViniRFB » Dom Fev 19, 2012 22:26
- 9 Respostas
- 5523 Exibições
- Última mensagem por ViniRFB

Ter Fev 21, 2012 20:05
Sistemas de Equações
-
- Razão e Proporção
por acalves » Ter Abr 03, 2012 22:52
- 4 Respostas
- 4558 Exibições
- Última mensagem por DanielFerreira

Qui Abr 05, 2012 01:29
Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Acrescentando-se 2 a cada um, as somas ficarão na razão 3 para 5. Calcule o produto dos números.
. Acrescentando-se 2 a cada um, as somas ficarão na razão 3 para 5. Calcule o produto dos números.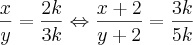
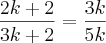
 ?!?!?!
?!?!?!
 . Acrescentando-se 2 a cada um, as somas ficarão na razão 3 para 5. Calcule o produto dos números.
. Acrescentando-se 2 a cada um, as somas ficarão na razão 3 para 5. Calcule o produto dos números.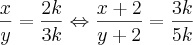
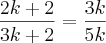
 ?!?!?!
?!?!?!



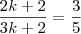
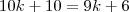

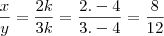




 .
.
 :
: