Guilherme Carvalho escreveu:1- Mostre que

e

Basta aplicar as definições para essas operações.
Lembre-se que dada uma matriz X, dizemos que

é o seu termo na posição da linha i e coluna j.
Temos então as seguintes definições.
1) Seja S = X + Y. Temos que
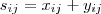
. (Aqui X e Y devem ser matrizes com mesma ordem).
2) Seja
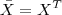
. Temos que

.
3) Seja P = XY. Temos que:
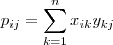
. (Aqui o número de colunas de X deve ser igual ao número de linhas de Y. Estamos supondo que esse número é n).
Por exemplo, vejamos a prova para a primeira identidade.
Seja S = A + B. Temos que
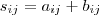
.
Seja
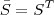
. Temos que

.
Por outro lado, sejam

e

. Se
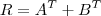
, temos que
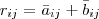
.
Lembrando que

e

, temos que

.
Conclusão: os termos da matriz
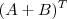
são os mesmos da matriz

. Isto é, temos que

.
Agora tente provar a segunda identidade.
Guilherme Carvalho escreveu:2- Uma matriz B é dita simétrica quando

. Mostre que A é B são simétricas e que A+kB é simétrica para todo k pertencente ao reais. Será AB simétrica?
Eu presumo que o texto original seja algo como:
2- Uma matriz B é dita simétrica quando

. Mostre que se A e B são simétricas, então A+kB é simétrica para todo k pertencente ao reais. Será AB simétrica?
Aqui basta aplicar os resultados já provados no exercício 1). Mas tem um detalhe: você vai precisar provar que

, com
k um número real qualquer. Além disso, lembre-se de mais outro detalhe: a multiplicação de matrizes não é comutativa. Isto é,
nem sempre é verdade que AB = BA.
 e
e 
 . Mostre que A é B são simétricas e que A+kB é simétrica para todo k pertencente ao reais. Será AB simétrica?
. Mostre que A é B são simétricas e que A+kB é simétrica para todo k pertencente ao reais. Será AB simétrica? e
e 
 . Mostre que A é B são simétricas e que A+kB é simétrica para todo k pertencente ao reais. Será AB simétrica?
. Mostre que A é B são simétricas e que A+kB é simétrica para todo k pertencente ao reais. Será AB simétrica? é o seu termo na posição da linha i e coluna j.
é o seu termo na posição da linha i e coluna j.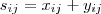 . (Aqui X e Y devem ser matrizes com mesma ordem).
. (Aqui X e Y devem ser matrizes com mesma ordem).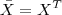 . Temos que
. Temos que  .
.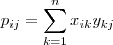 . (Aqui o número de colunas de X deve ser igual ao número de linhas de Y. Estamos supondo que esse número é n).
. (Aqui o número de colunas de X deve ser igual ao número de linhas de Y. Estamos supondo que esse número é n).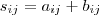 .
.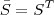 . Temos que
. Temos que  .
. e
e  . Se
. Se 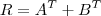 , temos que
, temos que 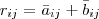 .
. e
e  , temos que
, temos que  .
.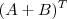 são os mesmos da matriz
são os mesmos da matriz  . Isto é, temos que
. Isto é, temos que  .
. , com
, com