-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478747 Mensagens
-
Última mensagem por admin
em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 535145 Mensagens
-
Última mensagem por admin
em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498720 Mensagens
-
Última mensagem por admin
em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 715288 Mensagens
-
Última mensagem por admin
em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2138330 Mensagens
-
Última mensagem por Janayna
em Qui Abr 27, 2017 00:04
 por Ana_Rodrigues » Qua Mar 14, 2012 17:14
por Ana_Rodrigues » Qua Mar 14, 2012 17:14
Qual a diferença entre a nulidade de uma matriz e a nulidade de um sistema?
Eu sei que a nulidade de um sistema vai indicar as possíveis (uma, infinitas ou nenhuma) soluções para esse sistema,porém não entendo pra que serve a nulidade de uma matriz, já que ambas são calculadas de maneira diferente.
Agradeço desde já, a quem me ajudar a entender!
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Mar 14, 2012 18:33
por MarceloFantini » Qua Mar 14, 2012 18:33
Você está possivelmente confundindo conceitos. A nulidade de uma matriz são as matrizes coluna

tais que

. Não existe conceito análogo para "nulidade" de um sistema.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ana_Rodrigues » Qua Mar 14, 2012 18:44
por Ana_Rodrigues » Qua Mar 14, 2012 18:44
Acho que eu não soube expressar minha dúvida.
Por onde eu estou estudando existem duas formas de calcular a nulidade de uma matriz:
N=n-p
onde:
n= numero de colunas da matriz
p= posto da matriz (que é o numero de linhas não nulas na matriz ampliada)
e
N=n-p
onde:
n=numero de incógnitas do sistema ou se preferir numero de incógnitas da matriz incógnitas
p= posto da matriz (neste caso há uma comparação entre o posto da matriz coeficiente e o posto da matriz ampliada).
Quero saber qual a diferença entre essas duas formas de calcular a nulidade, o que a primeira quer dizer?
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Mar 14, 2012 18:52
por MarceloFantini » Qua Mar 14, 2012 18:52
Um fato sobre matrizes é que o posto por linhas é igual ao posto por colunas. Ou seja, se você tem uma matriz não quadrada, seu posto será

se

for

com
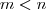
(nada de especial em ter menos linhas que colunas). Essas duas formas são equivalentes, a mesma maneira de dizer a mesma coisa. Mas a nulidade não diz se o sistema é impossível ou possível.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por caiou » Ter Jun 12, 2018 21:07
por caiou » Ter Jun 12, 2018 21:07
Você confundiu os conceitos, o segundo N= n-p, não é nulidade, e sim grau de liberdade.
-
caiou
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Jun 12, 2018 21:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharelado em sistema de informação
- Andamento: cursando
Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 tais que
tais que  . Não existe conceito análogo para "nulidade" de um sistema.
. Não existe conceito análogo para "nulidade" de um sistema.

 se
se  for
for  com
com 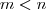 (nada de especial em ter menos linhas que colunas). Essas duas formas são equivalentes, a mesma maneira de dizer a mesma coisa. Mas a nulidade não diz se o sistema é impossível ou possível.
(nada de especial em ter menos linhas que colunas). Essas duas formas são equivalentes, a mesma maneira de dizer a mesma coisa. Mas a nulidade não diz se o sistema é impossível ou possível.